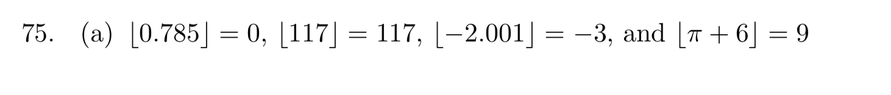Understanding the Floor Function: How to Find ⌊0.785⌋

[Yazan975]

I am not able to understand what the question asks of me in Q75, part a)
View attachment 9206View attachment 9207

 

[Evgeny.Makarov]

The problem asks you to find $$\lfloor 0.785\rfloor$$. The definition of $$\lfloor x\rfloor$$ for an arbitrary real $x$ is given in the first paragraph of the problem. If you don't understand that definition, I suggest an exchange. You give a detailed explanation of what you do and don't understand in that sentence. This helps me understand what parts of explanations may not be clear, and helps me hopefully explain things better in the future. In exchange, I describe the confusing parts. (I am not the author of the problem, of course.)

 

[HallsofIvy]

This is confusing! Yazan975 thanked Evgeny Makarov for his response but did not answer any of the questions or do any of the things that Evgeny Makarov suggested!