phantomvommand
- 287
- 39
- Homework Statement
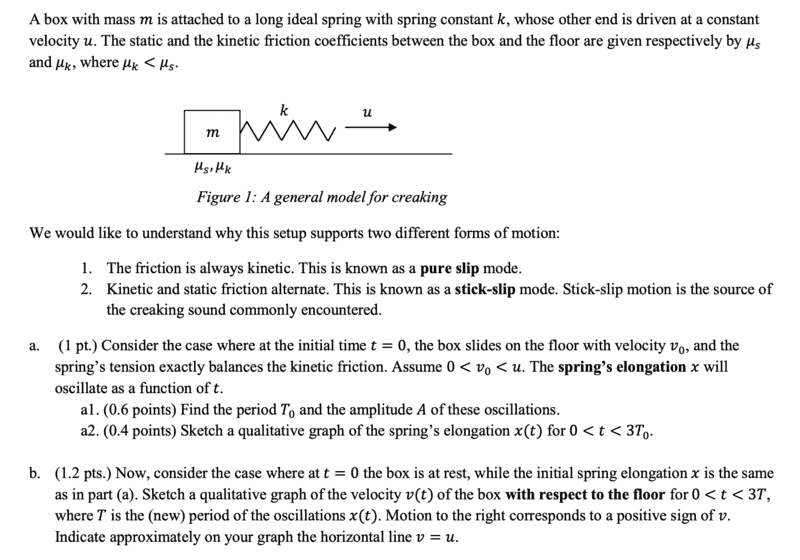
- Please see the attached photo
**I am only asking about the answer to part B, but please reading through part a may give some some context/familiarity.**
- Relevant Equations
- No equations required, but understanding SHM and Forces is important
I am only asking about the answer to part B, but reading through part A may give some some context/familiarity.
Below is the answer to part B:
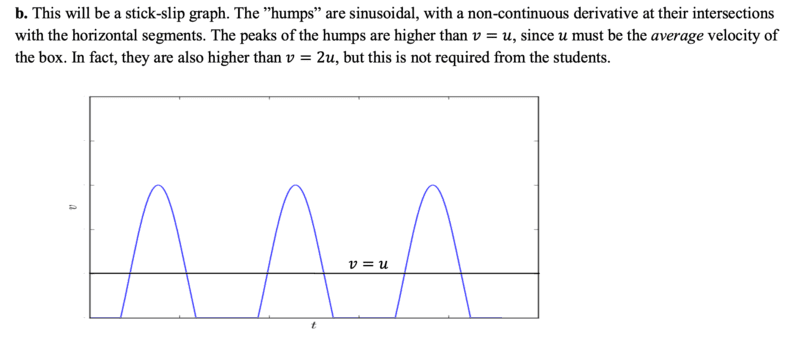
I largely understand the graph except for 1 part. My understanding is as such:
At first, ##x = \frac {\mu_k m g } {k}##. Force exerted by the extending spring is not enough to overcome the static friction.
Ater some time, force exerted is enough to overcome the static friction, resulting in velocity increasing.
However, the spring is still extending, because velocity of pulling > velocity of block.
When ##v = u##, maximum extension has been reached, maximum rightwards force on block.
At ##v = V_{max}##, ##\mu_k mg = kx##. After which, the net force on the block slows it down.
At ##v = u## again, the block has been slowed to speed ##u##, at which point no further compression can occur. (ie max compression)
Block is now pushed leftwards and slows down.
My question:
Why must the block slow down to speed 0, at which point static friction stops it from moving anymore? The point this occurs is when the spring is still compressed.
I am hoping to get a physical explanation of why the forces on the block slow it down to 0 velocity when the spring's compression ##= \frac {\mu_s m g } {k}##. I do not find the "symmetrical graph" argument convincing enough.
Below is the answer to part B:
I largely understand the graph except for 1 part. My understanding is as such:
At first, ##x = \frac {\mu_k m g } {k}##. Force exerted by the extending spring is not enough to overcome the static friction.
Ater some time, force exerted is enough to overcome the static friction, resulting in velocity increasing.
However, the spring is still extending, because velocity of pulling > velocity of block.
When ##v = u##, maximum extension has been reached, maximum rightwards force on block.
At ##v = V_{max}##, ##\mu_k mg = kx##. After which, the net force on the block slows it down.
At ##v = u## again, the block has been slowed to speed ##u##, at which point no further compression can occur. (ie max compression)
Block is now pushed leftwards and slows down.
My question:
Why must the block slow down to speed 0, at which point static friction stops it from moving anymore? The point this occurs is when the spring is still compressed.
I am hoping to get a physical explanation of why the forces on the block slow it down to 0 velocity when the spring's compression ##= \frac {\mu_s m g } {k}##. I do not find the "symmetrical graph" argument convincing enough.