- #1
tomtomtom1
- 160
- 8
Hi all
This is not a homework question but something work related which I am having difficulty understanding which I was hoping someone from the community could help me with.
I am trying to understand how to interpret & create the probability density function plot from a set of data.
For example:-
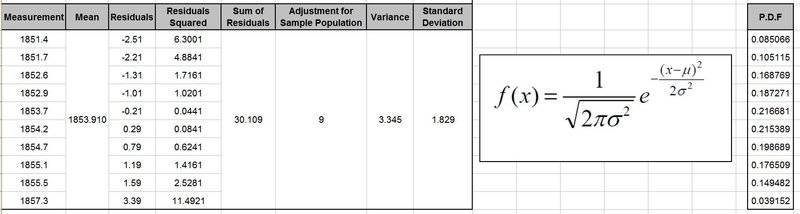
By plotting the measurements of my table (x) against the PDF (y) I get the following plot.
I know that to find the probability of a measurement of my table to fall between 1852 - 1855 for example then I would need to integrate the P.D.F from 1855 and subtract it from the integral of the PDF to 1852.
Hopefully I have got things correct so far.
The question is how do I adjust this graph and data so that the mean is exactly in the middle and the x values are 1 2 and 3 standard deviations as shown in the example plot below:-
I know this is a very long winded question but I could really appreciate your insight.
I have attached a note pad file that contains this data.
Many thanks.
This is not a homework question but something work related which I am having difficulty understanding which I was hoping someone from the community could help me with.
I am trying to understand how to interpret & create the probability density function plot from a set of data.
For example:-
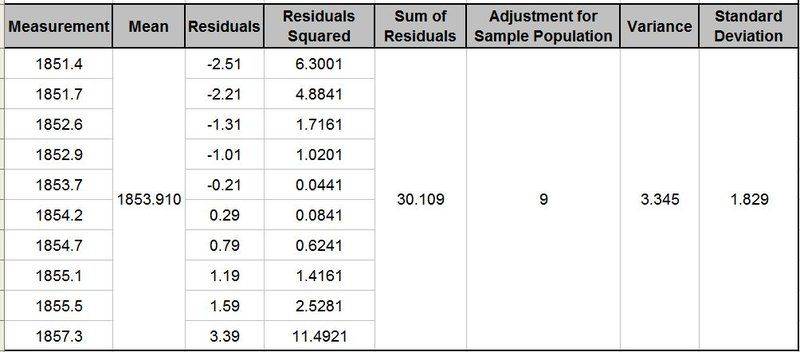
- Below is a set of measurements of the same table which I measured 10 times.
- As you can see I have calculated the Mean, Residuals, Squared the residuals and summed up the Squared Residuals.
- Because I can measure the table an infinite number of times (but impossible to do so) I only measured it 10 times, so 10 is my sample population and I have been told that I need to subtract 1 from the sample population which I have done so.
- I have then calculated the variance and standard deviation.
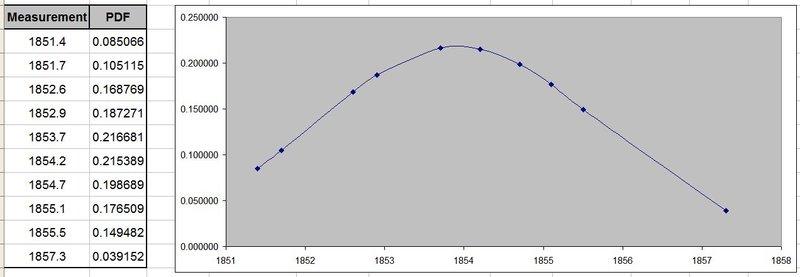
By plotting the measurements of my table (x) against the PDF (y) I get the following plot.
I know that to find the probability of a measurement of my table to fall between 1852 - 1855 for example then I would need to integrate the P.D.F from 1855 and subtract it from the integral of the PDF to 1852.
Hopefully I have got things correct so far.
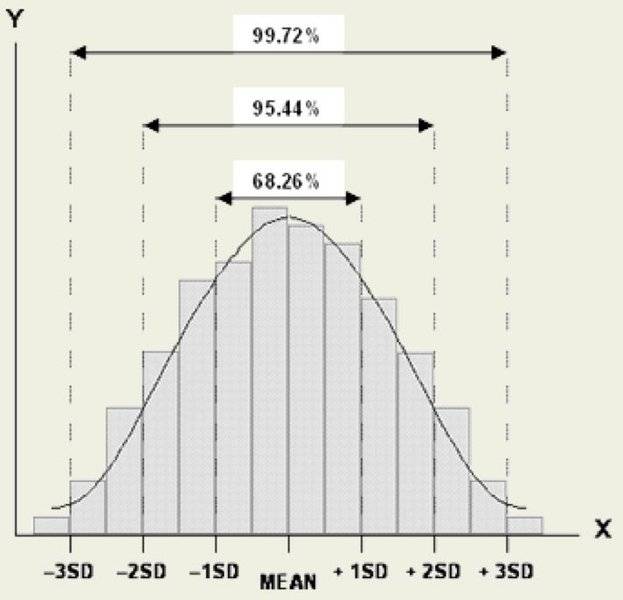
The question is how do I adjust this graph and data so that the mean is exactly in the middle and the x values are 1 2 and 3 standard deviations as shown in the example plot below:-
I know this is a very long winded question but I could really appreciate your insight.
I have attached a note pad file that contains this data.
Many thanks.