MaxJ
- 7
- 0
- Homework Statement
- Below
- Relevant Equations
- Below
For this problem,

The solution for (a) is
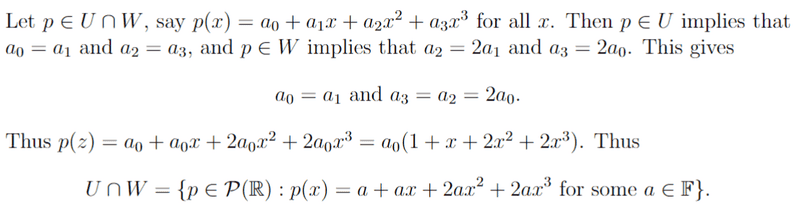
I am slightly confused for ##p \in W## since I get ##a_3 = 2a_1## and ##a_2 = 2a_0##. Since ##a_3 = 2b##, ##a_2 = 2a##, ##a_1 = b##, ##a_0 = a##.
Anybody have this doubt too?
Kind wishes
The solution for (a) is
I am slightly confused for ##p \in W## since I get ##a_3 = 2a_1## and ##a_2 = 2a_0##. Since ##a_3 = 2b##, ##a_2 = 2a##, ##a_1 = b##, ##a_0 = a##.
Anybody have this doubt too?
Kind wishes