Understanding the Sphere Rolling Problem: Simplifying the Equations

[Saitama]

Homework Statement

Homework Equations

The Attempt at a Solution

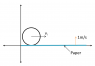
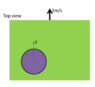
I have some difficulty understanding the problem statement. The problem says the paper moves horizontally but then in the very next line, it states the velocity is perpendicular to the initial velocity of sphere.

I can't visualize the motion of sphere. How to form the equations?

Any help is appreciated. Thanks!

 

[TSny]

Let the table be the x-y plane and let the initial velocity of the ball be along the x axis. The paper is then suddenly pulled in the y direction.

 

[Saitama]

Let the table be the x-y plane and let the initial velocity of the ball be along the x axis. The paper is then suddenly pulled in the y direction.

Hi TSny!

I drew a sketch, is it correct?

How to form the equations?

Thanks!

 

[voko]

There are two horizontal directions. The ball is rolling along one of those, the paper is moved along the other

 

[TSny]

The paper slides along the table in a direction perpendicular to the initial velocity of the ball. In your diagram, you would pull the paper either towards you (out of the screen) or away from you (into the screen).

 

[Saitama]

There are two horizontal directions. The ball is rolling along one of those, the paper is moved along the other

The paper slides along the table in a direction perpendicular to the initial velocity of the ball. In your diagram, you would pull the paper either towards you (out of the screen) or away from you (into the screen).

Okay, I understand the situation, thanks both of you but how to make the equations?

 

[Saitama]

I thought some more upon the problem. Please look at the attachment.

The green colour denotes the paper and the purple for sphere.

The $v_i$ remains unchanged as there is no force in that direction. The friction acts in the direction of paper's velocity.

Now I am confused at one point. I can easily find the velocity of sphere in the direction of paper's motion as $f=\mu_k mg$. Also, there will be angular velocity generated in a direction different to the initial one, so the final angular velocity is obtained by the resultant of two angular velocities. But then where do I need the coefficient of static friction ($\mu_s$)?

Am I heading in the correct direction?

 

[voko]

I agree with the outline of the solution. I do not think that static friction could play a role in this problem.

 

[TSny]

Maybe you won't need $\mu_s$. You'll have to work out the problem to see.

I think you are heading in the right direction.

 

[Saitama]

I agree with the outline of the solution. I do not think that static friction could play a role in this problem.

Maybe you won't need $\mu_s$. You'll have to work out the problem to see.

I think you are heading in the right direction.

Thanks a lot both of you.

Velocity after two direction in the motion of paper is $\mu_k gt=0.8g$.
Hence, resultant velocity is $\sqrt{v_i^2+(0.8g)^2}$

Similarly, I found the final (resultant) angular velocity to be
$$\sqrt{\left(\frac{v_i}{R}\right)^2+\left(\frac{2g}{R}\right)^2}$$

Should I use conservation of angular momentum now?

 

[TSny]

You can't assume that the friction force will last for 2.0 seconds. Can you see the condition that will determine when the friction force stops?

 

[Saitama]

You can't assume that the friction force will last for 2.0 seconds. Can you see the condition that will determine when the friction force stops?

When the pure rolling starts. Then what is the implication of 2 seconds in the problem?

 

[voko]

You should realize that as the paper stops, the sphere's velocity w.r.t. the paper changes abruptly again.

 

[Saitama]

You should realize that as the paper stops, the sphere's velocity w.r.t. the paper changes abruptly again.

I am not sure but do you mean that the frictional force reverses its direction after two seconds?

 

[TSny]

When the pure rolling starts. Then what is the implication of 2 seconds in the problem?

You will need to find the time the friction must act to produce rolling without slipping on the paper and make sure it's less than 2 seconds.

 

[haruspex]

You can break the problem into two parts: what is the velocity as it leaves the paper, then what is the final velocity. The second part is a standard question I'm sure you've seen before; it turns out to be independent of the coefficient of friction there (as long as it's not zero).

Conservation of momentum (linear and angular) is definitely the way to go. You can calculate how long before the sphere is rolling on the paper. While still sliding on the paper what is the torque? If it slides for time Ts, what angular velocity will it then have perpendicular to the movement of the paper (i.e perpendicular to its original axis of rotation)? What linear velocity (in the ground frame) in the direction of movement of the paper? What velocity in that direction relative to the paper? If it now starts rolling, what is the relationship between the angular and linear velocities?
Note that you can do all this in regard to the one spatial dimension, so no need to get tangled up with Pythagoras.

 

[Saitama]

You can break the problem into two parts: what is the velocity as it leaves the paper, then what is the final velocity. The second part is a standard question I'm sure you've seen before; it turns out to be independent of the coefficient of friction there (as long as it's not zero).

Conservation of momentum (linear and angular) is definitely the way to go. You can calculate how long before the sphere is rolling on the paper. While still sliding on the paper what is the torque? If it slides for time Ts, what angular velocity will it then have perpendicular to the movement of the paper (i.e perpendicular to its original axis of rotation)? What linear velocity (in the ground frame) in the direction of movement of the paper? What velocity in that direction relative to the paper? If it now starts rolling, what is the relationship between the angular and linear velocities?
Note that you can do all this in regard to the one spatial dimension, so no need to get tangled up with Pythagoras.

You will need to find the time the friction must act to produce rolling without slipping on the paper and make sure it's less than 2 seconds.

Here's what I think:

The velocity in the direction of motion of paper at any time t is $\mu_k gt$.

The angular velocity is $\mu_k mgR/(2/5 mR^2) t=(5/2)\mu_k gt/R$.

When pure rolling starts, we have the condition that $v+r\omega=1$
$$\mu_k gt+\frac{5}{2}\mu_k gt=1 \Rightarrow t=0.07288 \,\, \text{seconds}$$

This is less than 2 seconds so the pure rolling starts before the paper stops.

For the time calculated above, the velocity is $(2/7) m/s$ and angular velocity is $(5/(7R)) rad/s$.

When the paper stops, we apply conservation of angular momentum,
$$mvr-I\omega=mv'R+I\omega \Rightarrow \frac{2}{7}mR-\frac{2}{5}mR^2\frac{5}{7R}=mv'R+\frac{2}{5}mR^2\frac{v'}{R}$$
Solving for v' gives zero.

 

[nil1996]

Here's what I think:

The velocity in the direction of motion of paper at any time t is $\mu_k gt$.

The angular velocity is $\mu_k mgR/(2/5 mR^2) t=(5/2)\mu_k gt/R$.

When pure rolling starts, we have the condition that $v+r\omega=1$
$$\mu_k gt+\frac{5}{2}\mu_k gt=1 \Rightarrow t=0.07288 \,\, \text{seconds}$$

This is less than 2 seconds so the pure rolling starts before the paper stops.

For the time calculated above, the velocity is $(2/7) m/s$ and angular velocity is $(5/(7R)) rad/s$.

When the paper stops, we apply conservation of angular momentum,
$$mvr-I\omega=mv'R+I\omega \Rightarrow \frac{2}{7}mR-\frac{2}{5}mR^2\frac{5}{7R}=mv'R+\frac{2}{5}mR^2\frac{v'}{R}$$
Solving for v' gives zero.

i am too trying to solve this
can't Rω = 1cm/s be the condition for pure rolling?
where ω is the angular velocity due to the friction force perpendicular to the intial angular velocity.
by doing that i get t=0.103 s

 

[TSny]

Here's what I think:

The velocity in the direction of motion of paper at any time t is $\mu_k gt$.

The angular velocity is $\mu_k mgR/(2/5 mR^2) t=(5/2)\mu_k gt/R$.

When pure rolling starts, we have the condition that $v+r\omega=1$
$$\mu_k gt+\frac{5}{2}\mu_k gt=1 \Rightarrow t=0.07288 \,\, \text{seconds}$$

This is less than 2 seconds so the pure rolling starts before the paper stops.

Good.

For the time calculated above, the velocity is $(2/7) m/s$ and angular velocity is $(5/(7R)) rad/s$.

When the paper stops, we apply conservation of angular momentum,
$$mvr-I\omega=mv'R+I\omega \Rightarrow \frac{2}{7}mR-\frac{2}{5}mR^2\frac{5}{7R}=mv'R+\frac{2}{5}mR^2\frac{v'}{R}$$
Solving for v' gives zero.

What is the answer to the original question based on this result?

 

[Saitama]

What is the answer to the original question based on this result?

The answer is 1 which is correct. Interesting.

Can this be explained through the use of words? I mean, the final speed is unaffected by the motion of paper, is there a interpretation for this interesting result?

Thanks a lot everyone.

 

[TSny]

Here's a wordy way to look at it. (Too wordy, probably)

Let the x-axis be along the initial direction of the motion of the ball.

Choose an inertial frame of reference moving relative to the table in the x direction such that in this frame the ball initially has zero translational velocity (but is spinning about an axis in the y direction). You can pick a fixed origin in this frame such that there is never any torque about this origin on the ball due to the friction forces parallel to the y axis.

So, in this frame, the final angular momentum about the origin must be equal to the initial angular momentum. So, if the ball picks up any translational velocity v_y in the y direction due to the friction force, there must be a "backward" spin that the ball also picks up so that the translational angular momentum is canceled by the spin angular momentum. See attachment. The spin that the ball initially had at the beginning (about an axis parallel to the y-axis) stays constant throughout the problem and is not shown in the attachment.

But, after everything is over, the ball must end up rolling without slipping relative to the table. This requires any spin that is picked up due to the friction forces to be "forward" rather than "backward". So, the only possibility is for the ball to end up not picking up any velocity component parallel to the friction force.

 

[Saitama]

Thanks a lot TSny for such a nice explanation!

 

[voko]

There is a simpler solution, which I also think is easier to understand.

I will ignore the components of velocity of the ball that are perpendicular to the motion of paper.

While the ball is skidding on the paper, it experiences the force of friction $F$. This force is constant till skidding stops, then it is zero. If the ball has skidded for time $t$, $m (v_c - v_{c0}) = F t$ and $I (\omega - \omega_0) = R F t$, where $v_c$ is the velocity of the CoM w.r.t. the table, and $\omega$ is the angular velocity, and the zero subscript means "initial". Combined: $$

\frac {\omega - \omega_0} {v_c - v_{c0} } = \frac {mR} I = k $$

This equation holds for both motions: when the paper is pulled and when it is held. In the first motion, $\omega_0 = 0, \ v_{c0} = 0$, so $\omega_1 = k v_{c1}$. The second motion continues till skidding stops, which means $v_{c2} + R \omega_2 = 0$, hence $\omega_2 - \omega_1 = k (v_{c2} - v_{c1})= \to -v_{c2}/R - k v_{c1} = k (v_{c2} - v_{c1}) \to v_{c2} = 0$.

Observe that the result is independent of how long the paper was pulled, with what speed it was pulled, the mass and size of the ball and the coefficients of friction. In simpler terms it can be perhaps rephrased this way: when the paper is pulled, the ball gains some velocity, and, proportionally, angular velocity. When the paper is held, the ball finds itself spinning in the wrong direction, so it loses its angular velocity via friction, which results in a proportional decrease in linear velocity.

 

[Saitama]

There is a simpler solution, which I also think is easier to understand.

I will ignore the components of velocity of the ball that are perpendicular to the motion of paper.

While the ball is skidding on the paper, it experiences the force of friction $F$. This force is constant till skidding stops, then it is zero. If the ball has skidded for time $t$, $m (v_c - v_{c0}) = F t$ and $I (\omega - \omega_0) = R F t$, where $v_c$ is the velocity of the CoM w.r.t. the table, and $\omega$ is the angular velocity, and the zero subscript means "initial". Combined: $$

\frac {\omega - \omega_0} {v_c - v_{c0} } = \frac {mR} I = k $$

This equation holds for both motions: when the paper is pulled and when it is held. In the first motion, $\omega_0 = 0, \ v_{c0} = 0$, so $\omega_1 = k v_{c1}$. The second motion continues till skidding stops, which means $v_{c2} + R \omega_2 = 0$, hence $\omega_2 - \omega_1 = k (v_{c2} - v_{c1})= \to -v_{c2}/R - k v_{c1} = k (v_{c2} - v_{c1}) \to v_{c2} = 0$.

Observe that the result is independent of how long the paper was pulled, with what speed it was pulled, the mass and size of the ball and the coefficients of friction. In simpler terms it can be perhaps rephrased this way: when the paper is pulled, the ball gains some velocity, and, proportionally, angular velocity. When the paper is held, the ball finds itself spinning in the wrong direction, so it loses its angular velocity via friction, which results in a proportional decrease in linear velocity.

Thank you voko! This is great. :)