Understanding the Statement Circled in Red: Solving a Problem

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

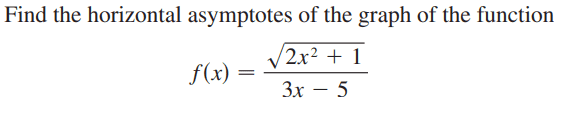
The solution is

However, I don't understand the statement circled in red. I don't understand why $x = - \sqrt{x^2}$? They did not explained why.

I remember a year ago a calculus teacher showed me how to solve this type of problem. They divided the numerator by $\sqrt{(-x)^2} = \sqrt{(x)^2}$ and the denominator by $-x$. I don't know why you have to divide by negative x for x approaches negative infinity, but this method works and give me the same result as the books method.

Many thanks!

 

[FactChecker]

Remember that this is the case where $x\lt 0$. Therefore, $-x$ is positive and $-x = |x| = \sqrt{x^2}$.

 

[member 731016]

Remember that this is the case where $x\lt 0$. Therefore, $-x$ is positive and $-x = |x| = \sqrt{x^2}$.

Thank you for your reply @FactChecker!

I think I understand now :)

 

[Mark44]

I remember a year ago a calculus teacher showed me how to solve this type of problem. They divided the numerator by $\sqrt{(-x)^2} = \sqrt{(x)^2}$ and the denominator by $-x$.

You didn't say, but the teacher must have specified that x < 0. Otherwise $\sqrt{(-x)^2} \ne -x$, so the fraction would essentially be multiplied by -1, which changes the value of the fraction.

 

[FactChecker]

You didn't say, but the teacher must have specified that x < 0. Otherwise $\sqrt{(-x)^2} \ne -x$, so the fraction would essentially be multiplied by -1, which changes the value of the fraction.

Yes. The solution included in post #1 says "we must remember that for $x \lt 0$ ...".

 

[Mark44]

Yes. The solution included in post #1 says "we must remember that for $x \lt 0$ ...".

I understand that, but I was responding to the part where the OP was remembering an event from a year ago. It wasn't stated that the teacher had specified then that x must be negative.

 

[member 731016]

You didn't say, but the teacher must have specified that x < 0. Otherwise $\sqrt{(-x)^2} \ne -x$, so the fraction would essentially be multiplied by -1, which changes the value of the fraction.

Thank you for your replies @Mark44 and @FactChecker !

I think my teacher said divide by numerator and denominator by (-x)^n where n is the highest degree of the denominator for taking the limit as x approaches negative infinity.

Many thanks!

 

[Mark44]

I think my teacher said divide by numerator and denominator by (-x)^n where n is the highest degree of the denominator for taking the limit as x approaches negative infinity.

That's not what my comment was about. For $\sqrt{(-x)^2}$ to be equal to -x, the teacher must have said that x < 0.

 

[FactChecker]

teacher must have said that x < 0.

Yes, but if the teacher says "as x approaches negative infinity", as he did, that takes care of itself.

 

[member 731016]

Thank you for your help @Mark44 and @FactChecker !