- #1
Jhenrique
- 685
- 4
I'm trying solve this scheme:
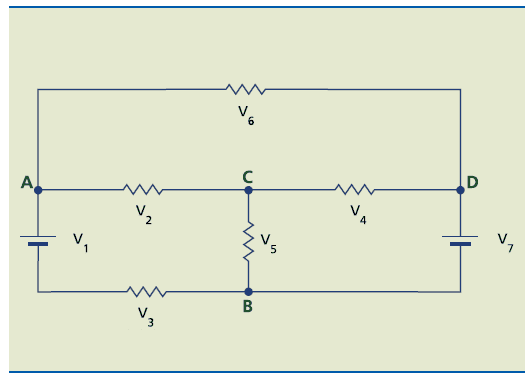
but not with the ideia of solve it but yes with the ideia of understand the dynamic of the thing...
aftwer watch this video:
and read about the superposition:
http://en.wikipedia.org/wiki/Superposition_theorem
I did this scheme for solve the problem:
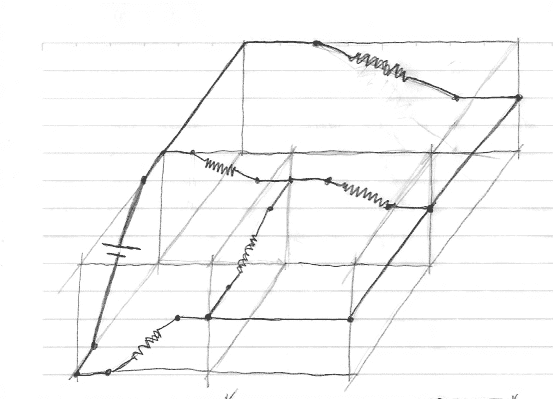
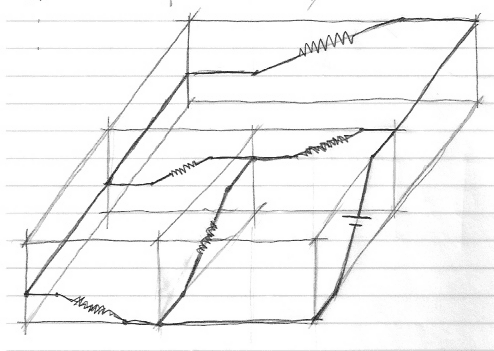
But, and now, how make the graphical superposition?
but not with the ideia of solve it but yes with the ideia of understand the dynamic of the thing...
aftwer watch this video:
and read about the superposition:
http://en.wikipedia.org/wiki/Superposition_theorem
I did this scheme for solve the problem:
But, and now, how make the graphical superposition?
Attachments
Last edited by a moderator:


