- #1
evinda
Gold Member
MHB
- 3,836
- 0
Hello! (Wave)
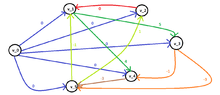
We construct the graph of a system of difference constraints like that:
Each vertex $v_i$ corresponds to one of the unknown variables.
Between the vertices $v_i$ and $v_j$ there is an edge iff $x_j-x_i \leq b_k$.
The weight of the edge $(v_i,v_j)$ is $b_k$.
At the graph of a system of difference constraints,we add an additional vertex $v_0$ and the edges $(v_0,v_1), (v_0,v_2), \dots, (v_0,v_n)$ with weight $0$.
Could you explain me the following theorem? (Thinking)
Let $G$ the graph,that corresponds to the problem $Ax \leq b$.If $G$ does not contain negative weight cycles,then a feasible solution of $Ax \leq b$ is this:
$$x=(\delta(v_0,v_1),\delta(v_0,v_2), \dots, \delta(v_0,v_n))$$
If $G$ contains negative weight cycles ,then $Ax \leq b$ has no feasible solution.
We construct the graph of a system of difference constraints like that:
Each vertex $v_i$ corresponds to one of the unknown variables.
Between the vertices $v_i$ and $v_j$ there is an edge iff $x_j-x_i \leq b_k$.
The weight of the edge $(v_i,v_j)$ is $b_k$.
At the graph of a system of difference constraints,we add an additional vertex $v_0$ and the edges $(v_0,v_1), (v_0,v_2), \dots, (v_0,v_n)$ with weight $0$.
Could you explain me the following theorem? (Thinking)
Let $G$ the graph,that corresponds to the problem $Ax \leq b$.If $G$ does not contain negative weight cycles,then a feasible solution of $Ax \leq b$ is this:
$$x=(\delta(v_0,v_1),\delta(v_0,v_2), \dots, \delta(v_0,v_n))$$
If $G$ contains negative weight cycles ,then $Ax \leq b$ has no feasible solution.