- #1
tomtomtom1
- 160
- 8
- TL;DR Summary
- Understanding the Value of the Second Moment Of Area
Hi all
I was hoping someone could help shed some light clearing some doubt on 2nd Moment of Area.
I know that if i had a beam that was loaded then the top of the beam would experience compressive forces.
As i moved down towards the neutral axis these compressive forces would become zero.
And i as i moved towards the bottom of the beam then the beam experiences tensile forces.
I know that the 2nd moment of area is how the area of a cross section is spread from the neutral axis i. e the more area away from the neutral
axis the less bending the beam will experience.
This is where i get confused.
Given a a rectangle (Breath 3m, Height= 7m), the equation for 2nd moment of area is given by bh^3/12 so my value for the second moment of area is 85.75m^4 as shown below:-
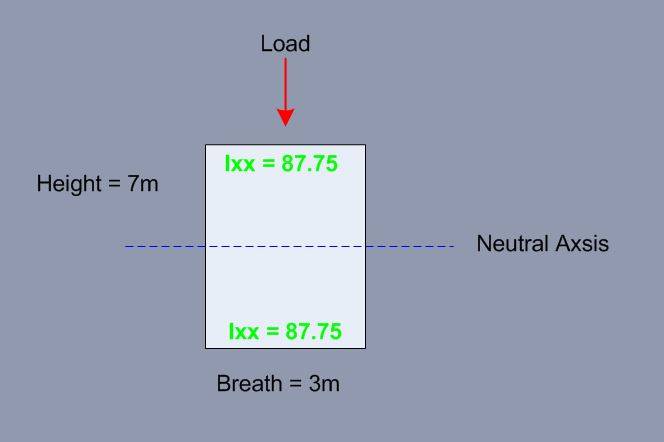
I am trying to visualize what this number means?
Does 85.75 mean that i have 87.75m^4 of area above AND below the neutral axis as shown in green above?
Or
Does 87.75 mean that my total area furthest away from the neutral axis is 87.75?
Finally does the equation Ixx = bh^3/12 only apply to a single point which is at the centriod or along the neutral axis in the cross section?
Can anyone help?
Thank you.
I was hoping someone could help shed some light clearing some doubt on 2nd Moment of Area.
I know that if i had a beam that was loaded then the top of the beam would experience compressive forces.
As i moved down towards the neutral axis these compressive forces would become zero.
And i as i moved towards the bottom of the beam then the beam experiences tensile forces.
I know that the 2nd moment of area is how the area of a cross section is spread from the neutral axis i. e the more area away from the neutral
axis the less bending the beam will experience.
This is where i get confused.
Given a a rectangle (Breath 3m, Height= 7m), the equation for 2nd moment of area is given by bh^3/12 so my value for the second moment of area is 85.75m^4 as shown below:-
I am trying to visualize what this number means?
Does 85.75 mean that i have 87.75m^4 of area above AND below the neutral axis as shown in green above?
Or
Does 87.75 mean that my total area furthest away from the neutral axis is 87.75?
Finally does the equation Ixx = bh^3/12 only apply to a single point which is at the centriod or along the neutral axis in the cross section?
Can anyone help?
Thank you.