Understanding the Wave Nature of Photons in Double Slit Experiments

[DParlevliet]

Yes, if amplitude in English is the maximum of the sinus.

 

[Cthugha]

So to come back to the start of this topic: what is the shape.

You have been given the answer before. There is absolutely no intrinsic shape of a photon. It really depends only on geometry. This is completely equivalent to the classical electromagnetic field. You can get any shape that is possible for a classical field also for a single photon. In fact, the probability amplitudes on the single photon level and the classical fields will usually look exactly the same. You can even give a single photon arbitrary shaping by pulse shaping it like a classical light pulse (see Specht et al., "Phase shaping of single-photon wave packets", Nature Photonics 3, 469 - 472 (2009)http://www.nature.com/nphoton/journal/v3/n8/abs/nphoton.2009.115.html)

This is somewhat complicated for extended geometries as changes in the field travel at the speed of light and you need to be able to create quite some large uncertainty in the exact time of emission (long coherence) to be able to achieve that.

 

[Naty1]

DParlevliet: a note of caution...I already posted this stuff is a bit 'crazy'...You cannot get a single all encompassing explanation of 'what particle looks like'...nor 'shape of a photon wave'. What the wave equation 'means' remains a debate.

A particle has no size at detection...it is a point particle. How do you describe such a thing in words. Nobody knows what a particle looks like between detections. The wave function and wave packets are our abstract attempts to quantify the evolution of a particle in time. Usually in abstract Hilbert space.

Be cautious about thinking the wave packet animation is 'what a particle looks like'; be cautious when thinking the wave is a means of physical interaction. As craigi already posted, the wave function is generally thought of as a probability of locating the 'particle'. One way to think about this crazy situation is that the center of a wave packet acts as a classical point particle.

But the wave is NOT classical, not observable: A wave function [like the Schrodinger one] (also more appropriately named as statefunction) in quantum mechanics describes the quantum state of a particle and how it behaves. Typically, its values are complex numbers. The probability is given by the product of the quantum state times it’s complex conjugate…because that WORKS...there are no first principles from which that crazy process can be developed. That is where our representation goes from deterministic to probabilistic.
In quantum field [wave] theory, modes with positive frequencies correspond [represent] real particles, those with negative frequencies correspond to antiparticles, and complex numbers correspond to virtual particles.

So all the prior posts should be taken in the limited context of how we model particle characteristics between detections rather than some exact physical picture.

 

[craigi]

... Nobody knows what a particle looks like between detections ...

I'd go even further than that. I'd say it doesn't look like anything. It can't, by definition, because to look at it would involve detection and we know it isn't the same as when it's detected.

 

[Naty1]

I posted...

...be cautious when thinking the wave is a means of physical interaction.

I see I left out a corresponding thought:
the 'wave' can't be physical, limited to speed 'c' because as craigi posted it seems to extend to infinity...so entanglement [faster than 'c' effects] become problematic... The extension of the wave to the cosmological horizon during inflation [which causes particle production] would never have produced photons [CMBR] because that horizon was receding faster than 'c'...

so the 'wave' and wave packet remain enigmatic.

 

[DParlevliet]

The double slit measures the wave, so there is only the wave, not the particle. So I don't ask what the particle is, I don't ask what the wave is, I just ask about its shape.
This

is good enough for me. It is an accurate image of the formulae (Schrodinger solution, Wiki). But what is the Schrodinger solution for a photon. The geometry is explained before.

So finally: the interference pattern shows that the shape of the wave of one photon is stable and predictable, when seen as an approximation. Does anyone know this shape?

 

[Bill_K]

So finally: the interference pattern shows that the shape of the wave of one photon is stable and predictable, when seen as an approximation. Does anyone know this shape?

You still don't get it, DParlevliet. You still don't get it. All right, suppose we tell you the shape is a Gaussian.

 

[Naty1]

Just for clarity, not to pick pick:

The double slit measures the wave, so there is only the wave, not the particle.

No. No one has posted such a thing. Any measurement is pointlike localized particle.

the interference pattern shows that the shape of the wave of one photon is stable

No. it depends on geometry...There is a graphical illustration of a different sort of what happens to be a matter wave here...at the top of the page on the right in yellow and blue:

Matter wave
http://en.wikipedia.org/wiki/De_broglie_wavelength

It illustrates the real and imaginary components of the location probability amplitude I mentioned earlier.

Note again this is a description of location probability NOT the 'shape' of the matter particle itself.

I hope I mentioned in my first post the necessity for rereading explanations such as these posts several times so you [anyone] can absorb it; You have to change the way you think when moving from classical to quantum realms.

Maybe try rereading slowly, reviewing carefully, from the beginning?...or try searching and reading some other discussions here...or Wikipedia explanations...

good luck...

 

[craigi]

The double slit measures the wave, so there is only the wave, not the particle. So I don't ask what the particle is, I don't ask what the wave is, I just ask about its shape.
This

is good enough for me. It is an accurate image of the formulae (Schrodinger solution, Wiki). But what is the Schrodinger solution for a photon. The geometry is explained before.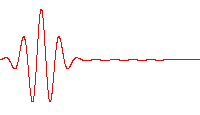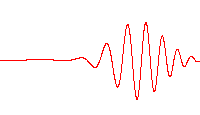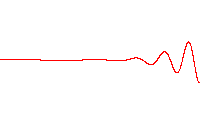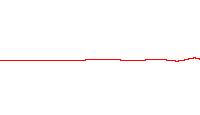

So finally: the interference pattern shows that the shape of the wave of one photon is stable and predictable, when seen as an approximation. Does anyone know this shape?

The animation that you have have there is like an artistic representation of photon. Let's take a look at what you can take from it and what you shouldn't.

Firstly it's one dimensional. Real photons exist in three dimensions. The vertical dimension is what they're using to depict the quantities that it's carrying, like when you plot a value on a graph.

The envelope (the Gaussian), is a plausible depiction, for the probability of finding a photon at a particular positon. It's just an example. Not all photons can be found with that probability distribution.

The envelope is moving forward, indicating that it represents a freely moving particle, with a precise momentum. If the photon were to interact geometrically or there were uncertainty about its momentum, that envelope would be different. Though in this case, the depiction is one dimensional, so the momentum must be a constant, though there are arrangements that could split it.

The wave pattern in the middle of the envelope is an artisic representation of the wavelength of the electromagnetic radation transmitted by that photon. That wavelength is relevant when the photon interacts with other photons and charged particles.

Because the photon has zero rest mass and travels at the speed of light, there is no solution to the Schrodinger equation for a photon.

A photon is a particle of electromagnetic radation. The understanding of this predates quantum physics. It can tell you more about what photons actually carry, than you would typically learn from quantum mechanics http://en.wikipedia.org/wiki/Electromagnetic_radiation.

I know this doesn't answer the question in the manner which you'd like. Perhaps, it would be more meaningful to ask about the geometrical arrangements that do and don't give rise to single photon self-interference due to time seperation.

Finally, I'd like to say: don't be demoralised, if you're struggling to get your head around it. Learning about QM is as much about unlearning as it is learning.

 

[Naty1]

I came across this description...about how difficult it is to describe the wavefuntion...wave packet, etc...

Schrodinger was smart enough the develop his "Schrodinger wave equation" based on the particle/wave duality of de Broglie, to show his equation equivalent to the other major formulation of the day, , the matrix mechanics of Heisenberg, even formulate what became the Klein-Gorden equation, but could not apparently change his way of thinking enough to adapt to the new insights available! http://en.wikipedia.org/wiki/Schrödinger_equation#Historical_background_and_development

The Schrödinger equation details the behavior of ψ but says nothing of its nature. Schrödinger tried to interpret it as a charge density in his fourth paper, but he was unsuccessful.[18] In 1926, just a few days after Schrödinger's fourth and final paper was published, Max Born successfully interpreted ψ as the probability amplitude, whose absolute square is equal to probability density.[19] Schrödinger, though, always opposed a statistical or probabilistic approach, with its associated discontinuities—much like Einstein, who believed that quantum mechanics was a statistical approximation to an underlying deterministic theory— and never reconciled with the Copenhagen interpretation.[20]
Louis de Broglie in his later years has proposed a real valued wave function connected to the complex wave function by a proportionality constant and developed the De Broglie–Bohm theory.

 

[jartsa]

If the shape of the wave envelope is such that there are sharp corners, then it's not possible to produce an interference pattern were there is complete cancellation somewhere.

Because the wavelength in uncertain.

I mean complete cancelleation of all the possible waves with different wavelengths is impossible.

Actually wavelength is always somewhat uncertain, so complete cancellation is never possible, I guess.

 

[DParlevliet]

I am not struggling to get my head around QM, but to construct questions and traps to get something out of here. But you don't know and are not interested in the answer. Probably it is too basic, to simple, you only go for answers which covers the whole universe (and outside). So this is not the right place.

The wave is clearly visible for everyone who looks to the double slit experiment. It is the interference pattern. That is the shape, the envelope. Most photons which are absorbed by the detector had this shape when they entered the slits (the rest are for you). With different geometry's you will find the same pattern. Of course there must a formula which describes this as an approximate. But I will not find that here.

But still thanks for all your answers and effort. I still learned from it (although less about QM).

 

[Cthugha]

I am not struggling to get my head around QM, but to construct questions and traps to get something out of here. But you don't know and are not interested in the answer.

You have been given the answer several times. You just do not like it. We cannot help with that. You do not even need to wrap your head around QM. The math is exactly the same as for the double slit in classical optics.

The wave is clearly visible for everyone who looks to the double slit experiment. It is the interference pattern. That is the shape, the envelope.

No. Not at all.

Most photons which are absorbed by the detector had this shape when they entered the slits (the rest are for you).

Also: no.

With different geometry's you will find the same pattern.

Third no. Change the slit distance or their width and you will get a different pattern. Move the position of your light source and you will get a different pattern. If you move too close, you will even get no pattern at all. Change slit orientation and you will get a different pattern. The interference pattern is nothing but a map of the phase difference between two paths leading from the same initial point to the same end point. That is all there is to it. All that matters is the wavelength of the photon used. Besides that, ALL of the double slit pattern just depends on geometry.

 

[craigi]

I am not struggling to get my head around QM, but to construct questions and traps to get something out of here. But you don't know and are not interested in the answer. Probably it is too basic, to simple, you only go for answers which covers the whole universe (and outside). So this is not the right place.

The wave is clearly visible for everyone who looks to the double slit experiment. It is the interference pattern. That is the shape, the envelope. Most photons which are absorbed by the detector had this shape when they entered the slits (the rest are for you). With different geometry's you will find the same pattern. Of course there must a formula which describes this as an approximate. But I will not find that here.

But still thanks for all your answers and effort. I still learned from it (although less about QM).

Sorry dude, you still misunderstand it. Are you still in education? Has this subject cropped up at school/college/university yet?

The double slit experiment is usually not taught until the age of 16 or 17, though a good understanding of it, isn't expected until undergraduate level. Perhaps you need to wait a little while, or perhaps just keep reading, until it falls into place for you.

Do you have a book that covers the subject? I'd recommend using one, if not. Piecing together information from the internet isn't the best way to learn this stuff.

I know for a fact that many of the people in the quantum mechanics section of this forum, have a very good understanding of this subject, beyond anything you'll find from a teacher in High School.

 

[Naty1]

The animation posted above by Dparl is non relativistic:

[source is here:]

http://en.wikipedia.org/wiki/Schrödinger_wave_equation#Time-dependent_equation


Can someone explain how it is appropriate to be referencing such an illustration for light waves,that is photons? If it is ok, where does such a representation breakdown...

Wikipedia says it this way:


http://en.wikipedia.org/wiki/Relati...#Early_1920s:_Classical_and_quantum_mechanics

...the Schrödinger and Heisenberg formulations are non-relativistic, so they can't be used in situations where the particles travel near the speed of light, or when the number of each type of particle changes (which happens in real particle interactions; the numerous forms of particle decays, annihilation, matter creation, pair production, and so on).

 

[Naty1]

What does the following mean in the context of all the explanations in this thread??

http://en.wikipedia.org/wiki/Quantum_field_theory#Unification_of_fields_and_particles

Sometimes, it is impossible to define such single-particle states, and one must proceed directly to quantum field theory. For example, a quantum theory of the electromagnetic field must be a quantum field theory, because it is impossible (for various reasons) to define a wavefunction for a single photon. In such situations, the quantum field theory can be constructed by examining the mechanical properties of the classical field and guessing the corresponding quantum theory.

 

[Bill_K]

What does the following mean in the context of all the explanations in this thread??

This is what VanHees was referring to in #18 above - the impossibility of defining a position operator for a photon.

 

[Naty1]

This is what VanHees was referring to in #18 above -

Ah, I skimmed that post but did not get the context!

Thanks...