Understanding Time Measurement in Physics: Uncertainty and Calculations

[srnixo]

Homework Statement

I'm so confused how to calculate the uncertainties , i suggested a lot of methods i thought about, so please help me! i need a clear answers

Relevant Equations

.

So as you can see in the image, I have noted the time in the [time column (s) ] on the table after conducting the experiment at home using the application phyphox.

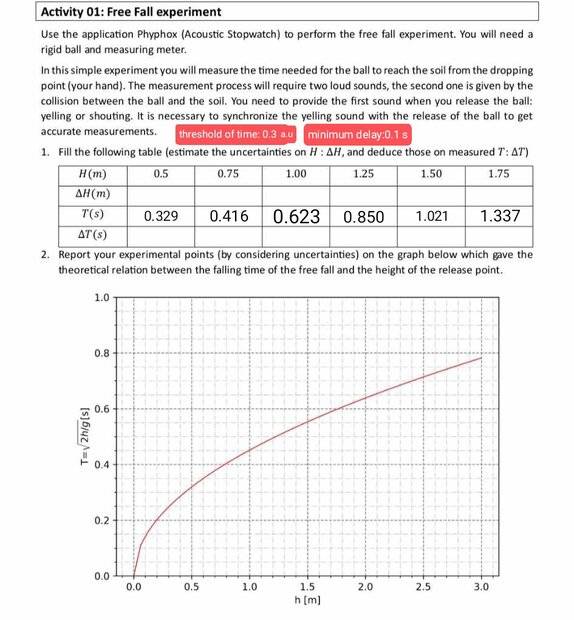
And now, I have some questions to fill in the remaining gaps:

The first question: about ΔH (m) :

• Should I set it equal to zero [ΔH=0] because I didn't calculate it, the values were directly given from the exercise?
• Or at least 0.1 [ΔH=0.1] due to the potential small error in the measurements of the used meter tool!
• 
  
• Or nevertheless, I must calculate it, and let that be in that way :[I don't know if it's correct or not, this is the only method i know]:
  
  
  
  
  ----------------------------------------------------------------------------------------------------------------------------
  The second question: about ΔT(s) :
  First of all, in the app phyphox of calculating the T , there were a choice of threshold and minimum delay, and as i mentioned:
  The threshold: 0.3 a.u ( i don't know what does a.u means! i don't even know which unit is that so i can't finish the calculations)
  The minimum delay: 0.1 s
• So, do i assume that the threshold corresponds to a time interval and i convert it to seconds so it becomes 0.003 seconds and then calculate it using [ Minimum delay + time interval ] which means [0.1+0.003= 0.103 seconds for all of them! ]
• Or i use the formula ΔT= threshold x measured time + minimum delay so that i keep threshold 0.3
• Or i calculate it in the same way previously , and i write the same result in all the gaps!
  
  

• Or there is another correct way? please help!​

 

[brainpushups]

This is likely the intention:
You need to estimate the uncertainty in height with a reasonable judgement call. How close do you think you were to each precise height you were supposed to drop the object from? I bet you were more careful than 0.1 meter for each height! Use a ruler to help you gauge your likely range if necessary.

With each height you need to calculate the time of fall. This is the prediction of how long it should take according to the free fall 'theory.' You'll compare this against the actual data you recorded for each time.

The formula you use to calculate each time is on the y axis of your graph. To get the uncertainty in time you propagate the uncertainty you estimated in height through the calculation. Hopefully you've been given resources on how to do this. But, if not, you can read about it readily online. If it is new to you, expect to spend a few hours reading and practicing before you feel confident in it.

Now that you have the experimental values of time (assumed to have negligible uncertainty compared to your uncertainty in height) and the theoretical values of time (based on the uncertainty in your measurement of height) you can make a meaningful comparison between the prediction and outcome.

 

[haruspex]

I largely agree with @brainpushups , but some things worry me.
The wording "uncertainties … in measured T" seems wrong if these are deduced from the intended h and the formula. They may be discrepancies or errors but not uncertainties. An uncertainty in a measurement of T would reflect differences between measured T and the actual time.
What are you expected to plot on the graph? The obvious way is to plot horizontal error bars $(T_i,[h_i-\Delta h, h_i+\Delta h])$. I don't see what the calculated $\Delta T$ adds.

From reading https://phyphox.org/wiki/index.php/Experiment:_Acoustic_Stopwatch, it seems the "threshold" is the minimum noise level (in some audio units) to register as a trigger and the minimum delay is the minimum time between the two sounds for the app to consider them as two triggers. You do not need to worry about these if it seems to be working.

 

[Tom.G]

Homework Statement: I'm so confused how to calculate the uncertainties , i suggested a lot of methods i thought about, so please help me! i need a clear answers
Relevant Equations: .

The threshold: 0.3 a.u ( i don't know what does a.u means! i don't even know which unit is that so i can't finish the calculations)

A.U. is "Arbitrary Units".
It seems to apply to the "gain" setting for the sound detector, with highest gain being 1.0. It just has to be high enough to get reliable sound triggering. It would not be involved in, or appear in, the required calculations.

Cheers,
Tom

irrelevant p.s. The A.U. abbreviation also shows up in Astronomy, but is defined there as "Astronomical Unit", the mean distance between the Earth and Sun.

 

[srnixo]

This is likely the intention:
You need to estimate the uncertainty in height with a reasonable judgement call. How close do you think you were to each precise height you were supposed to drop the object from? I bet you were more careful than 0.1 meter for each height! Use a ruler to help you gauge your likely range if necessary.

"But I didn't understand a simple thing, do all the values remain the same or do they change depending on each height?"
According to my knowledge, it depends on the meter tool used so normally the range is gonna be between 0.5 and 0.6 for all the heights isn't?

 

[brainpushups]

"But I didn't understand a simple thing, do all the values remain the same or do they change depending on each height?"
According to my knowledge, it depends on the meter tool used so normally the range is gonna be between 0.5 and 0.6 for all the heights isn't?

By "the values" do you mean the values of the uncertainty? That is up to you. I expect them to be similar, and perhaps the same, but that doesn't have to be the case.

For example, when you measure 0.50 meters and try to drop the object from that height did you do something like support the object on something like a clipboard right next to the meter stick's 0.5 meter mark and have very little 'wiggle' in your arm before dropping it? In that case I'd imagine that ± 0.005 m (half a centimeter) is a plausible range. Or were you less careful than that? If you just dropped it by holding it with your hand and were less steady, then maybe 0.01 or 0.02 meters (1 or 2 cm) is a more honest assessment of your uncertainty.

If you dropped the thing the same way for each height then I'd imagine that having the same absolute uncertainty (measured in m or cm) stays the same. There could be other factors to consider, like if you had to move the meter stick to measure 1.75 m, but I'd guess any other sources of error are negligible compared to your ability to hold the object still (provided they were done with care). The extra millimeter or two of uncertainty that moving a meter stick may introduce is insignificant compared to the half centimeter or more of uncertainty you judge.

Though the absolute uncertainty may stay the same note that your relative uncertainty in height will decrease. Let's assume you go with ±1 cm for a reasonable uncertainty. For the 50 cm drop that is a 2% relative uncertainty, but in the 100 cm drop it is only 1%. You'll end up using these percentages as part of the error propagation.

 

[srnixo]

For example, when you measure 0.50 meters and try to drop the object from that height did you do something like support the object on something like a clipboard right next to the meter stick's 0.5 meter mark and have very little 'wiggle' in your arm before dropping it? In that case I'd imagine that ± 0.005 m (half a centimeter) is a plausible range. Or were you less careful than that? If you just dropped it by holding it with your hand and were less steady, then maybe 0.01 or 0.02 meters (1 or 2 cm) is a more honest assessment of your uncertainty.

I got it right now, Thank you so much.