Understanding Work Integrals: Examples Explained

[Jefferson]

I have a question about work integrals. I'm trying to reconcile using integrals to essentially multiply force by distance, but the fact that there appear to be multiple different types of problems that seem to be fundamentally different is making it difficult. Here are some example problems:

Example 1.
A cable that weighs 8 lb/ft is used to lift 650 lb of coal up a mine shaft 700 ft deep. Find the work done.

Example 2:
A cylindrically shaped tube has a circular base with a diameter of 2 inches and a height of 12 inches. The bottom of the tube is closed. The tube contains a liquid which is 3 inches deep and has a weight density of 62 lbs per ft³. What is the work done in pumping the liquid to the top of the tube?

Example 3:
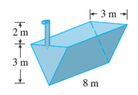
A tank is full of water. Find the work W required to pump the water out of the spout. (Use 9.8 m/s² for g. Use 1000 kg/m³ as the weight density of water.)
View attachment 1915

In the first example you find an equation for the force that is done and then integrate with bounds over the distance moved.

In the second example however, you find an equation for the distance a layer is moved, with a constant force multiplied in, and you integrate with bounds from one end of the substance to the other.

The third example seems to combine these two issues into one problem. In this case, the force equation and and the distance equation are multiplied together, but the bounds of integration are still over the substance moved and not the distance.

If someone could explain the differences in these problems, and what exactly the integration is adding up, I would much appreciate it. Specifically I would like to know why the first one integrates with bounds over the distance moved, and doesn't seem to include an equation for the distance in the integral (I'm guessing these are related, but I can't quite put my finger on exactly why), and why the second two examples integrate over the bounds of the substance moved instead.

 

[Ackbach]

Welcome to MHB! Thank you for posting such a well-worded problem.

Here's my answer: the work done by a force $ \mathbf{F}= \mathbf{F}( \mathbf{x})$ is given by
$$W= \int_{ \mathbf{a}}^{ \mathbf{b}} \mathbf{F} \cdot d\mathbf{l}.$$

This is a line integral over a particular path. So from this integral, you can see what needs to happen if the force is changing (such as it would for a spring, or for an irregular tank). But now suppose you can't ignore differences in path for different parts of your problem. You would then have to consider that the previous equation is only an infinitesimal chunk of work done by moving an infinitesimal chunk of stuff through its (now single) path:
$$dW= d \left( \int_{ \mathbf{a}}^{ \mathbf{b}} \mathbf{F} \cdot d\mathbf{l} \right).$$
Now, to find the total work done, you must integrate this expression:
$$W=\int_{\text{each path}}d \left( \int_{ \mathbf{a}}^{ \mathbf{b}} \mathbf{F} \cdot d\mathbf{l} \right).$$
This is what is really happening with your work problems.

One comment about your third problem: it will definitely have to have a distance moved in there somewhere. What expression do you get for the work done?

 

[Jefferson]

OK, I think I get some of what you are saying, but I'm still not totally clear. It is sort of like you are doing two integrals at the same time so that you can add up the two different quantities? What exactly is a line integral? Is the dl in the examples representing distance or is it the differential?

For example 3 I would integrate as follows:
\(\displaystyle
(9.8)(1000)\int_0^3 8x(5-x) \, dx\)
\(\displaystyle
(g)(\text{density of water}) \int_{\text{lower limit of substance}}^{\text{upper limit of substance}} (\text{area of a "layer"})(\text{distance the layer is moved}) \, dx\)

What it seems like this integral is doing is integrating to find the volume of the water and then multiplying that by density and gravity to give force and then multiplying by the distance. This must not be exactly right, though. I see that each layer has it's own path to travel, but I don't really get how this is added up in the integral.

Whereas example 1:
\(\displaystyle \int_0^{700} 8x +650 \, dx\)

\(\displaystyle \int_{\text{starting point}}^{\text{upper limit of movement}} (\text{the force on the rope, not exactly sure why x is included}) + (\text{force on the coal}) \, dx\)

It is much less visible to me what this integral does.

 

[Jefferson]

In case anyone is wondering I did finally find out how these problems are different. Some are using the definition of work as \(\displaystyle \int F \cdot \, ds\) whereas others, such as the tank problem, are using the definition of work as the potential energy change, i.e. \(\displaystyle E_f - E_i =\) Work, or \(\displaystyle mgh_f - mgh_i\). In the latter case the integral is adding up the work done in moving each layer from it's initial height to it's final height.

 

[Ackbach]

In case anyone is wondering I did finally find out how these problems are different. Some are using the definition of work as \(\displaystyle \int F \cdot \, ds\) whereas others, such as the tank problem, are using the definition of work as the potential energy change, i.e. \(\displaystyle E_f - E_i =\) Work, or \(\displaystyle mgh_f - mgh_i\). In the latter case the integral is adding up the work done in moving each layer from it's initial height to it's final height.

Right. Well, one of your fundamental physics laws is the Work-Energy Theorem:
$$W=\Delta PE + \Delta KE.$$
If your kinetic energy doesn't change, then the work you put into the system must increase the potential energy.