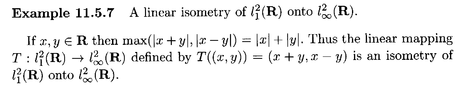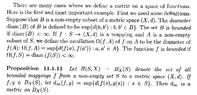MHB Uniform norm .... Garling Section 11.2 Normed Saces .... also Example 11.5.7

[Math Amateur]

I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume II: Metric and Topological Spaces, Functions of a Vector Variable" ... ...

I am focused on Chapter 11: Metric Spaces and Normed Spaces ... ...

I need some help in order to understand some remarks by Garling on the uniform norm made in Section 11.2 on page 311 and references made and notation used in Example 11.5.7 ... ...

The remarks by Garling made in Section 11.2 on page 311 ... ... read as follows:View attachment 9002... and Example 11.5.7 reads as follows ... ...View attachment 9003In the above remarks by Garling we read the following:

" ... ... We denote $$l_\infty ( \mathbb{N} )$$ ( or $$l_\infty ( \mathbb{Z}^{ + } )$$ ) by $$l_\infty$$, and $$l_\infty( \{ 1, \ ... \ ... \ , d \} )$$ by $$l^d_\infty$$. ... ... "

My issue/problem is that I'm not certain of the nature of $$l_\infty( \{ 1, \ ... \ ... \ , d \} )$$ or $$l^d_\infty$$ ... could someone please explain the nature of the normed space $$l_\infty( \{ 1, \ ... \ ... \ , d \} )$$ ... ...

On the face of it the normed space $$l_\infty( \{ 1, \ ... \ ... \ , d \} )$$ seems to me to be the set of all functions from the set $$\{ 1, \ ... \ ... \ , d \} \to \mathbb{R}$$ or $$\to \mathbb{C}$$ ... does that mean that say that $$f_1$$ picks a vector in $$\mathbb{R}^d$$ or $$\mathbb{C}^d$$ and $$f_2$$ picks (or maps to) a different vector etc ...

My problem in Example 11.5.7 is to make sense of $$l^2_1 ( \mathbb{R} )$$ and $$l^2_\infty ( \mathbb{R} )$$ ... can someone carefully explain the nature of these spaces ... and then explain the mapping $$T: l^2_1 ( \mathbb{R} ) \to l^2_\infty ( \mathbb{R} )$$ ...Hope someone can help ...

Peter==========================================================================================The above post mentions Proposition 11.1.11 ... so I am providing access to the same plus some relevant preliminary remarks ... as follows:
View attachment 9004
View attachment 9005

Hope that helps ... ...

Peter

 

[Opalg]

My issue/problem is that I'm not certain of the nature of $$l_\infty( \{ 1, \ ... \ ... \ , d \} )$$ or $$l^d_\infty$$ ... could someone please explain the nature of the normed space $$l_\infty( \{ 1, \ ... \ ... \ , d \} )$$ ... ...

In the notation $l^d_\nu$, the upper index $d$ denotes the dimension of the space. So $l^2$ just means $\Bbb{R}^2$ or $\Bbb{C}^2$, depending on whether the real or complex scalars are being used. The lower index $\nu$ (usually $1$, $2$ or $\infty$) tells you the norm that is being used. So for example $l^2_2(\Bbb{R})$ is just two-dimensional space with the euclidean distance $\|(x,y)\| = \sqrt{x^2+y^2}$ as the norm.

On the face of it the normed space $$l_\infty( \{ 1, \ ... \ ... \ , d \} )$$ seems to me to be the set of all functions from the set $$\{ 1, \ ... \ ... \ , d \} \to \mathbb{R}$$ or $$\to \mathbb{C}$$ ... does that mean that say that $$f_1$$ picks a vector in $$\mathbb{R}^d$$ or $$\mathbb{C}^d$$ and $$f_2$$ picks (or maps to) a different vector etc ...

When these spaces are described in terms of functions $f:S\to E$ (where $E = \Bbb{R}$ or $\Bbb{C}$), the set $S$ is just a set of $d$ elements, say $S = \{1,2,\ldots,d\}$. So an element of $l^2$ is a function $f$ from the set $\{1,2\}$ to $E$. If you write $f(1) = x$ and $f(2) = y$ then you can identify $f$ with $(x,y)$. In a finite-dimensional space, it may seem strange to think of points of the space as being functions. But in the case when $d = \infty$ it is natural to think of elements of $l^\infty$ as functions from the natural numbers to $E$.

My problem in Example 11.5.7 is to make sense of $$l^2_1 ( \mathbb{R} )$$ and $$l^2_\infty ( \mathbb{R} )$$ ... can someone carefully explain the nature of these spaces ... and then explain the mapping $$T: l^2_1 ( \mathbb{R} ) \to l^2_\infty ( \mathbb{R} )$$ ...

As I explained above, both $$l^2_1 ( \mathbb{R} )$$ and $$l^2_\infty ( \mathbb{R} )$$ are the space $\Bbb{R}^2$, but with different norms. For $l^2_1$, the norm is given by $\|(x,y)\|_1 = |x| + |y|$. For $l^2_\infty$, it is $\|(x,y)\|_\infty = \max\{|x|, |y|\}$.

In Example 11.5.7, the map $T:l^2_1 \to l^2_\infty$ is given by $T(x,y) = (x+y,x-y)$. The norm of $(x,y)$ in $l^2_1$ is $|x|+|y|$, and the norm of $T(x,y)$ in $l^2_\infty$ is $\max\{|x+y|,|x-y|\}$. Since those two expressions are equal, it follows that $T$ is an isometry.

 

[Math Amateur]

In the notation $l^d_\nu$, the upper index $d$ denotes the dimension of the space. So $l^2$ just means $\Bbb{R}^2$ or $\Bbb{C}^2$, depending on whether the real or complex scalars are being used. The lower index $\nu$ (usually $1$, $2$ or $\infty$) tells you the norm that is being used. So for example $l^2_2(\Bbb{R})$ is just two-dimensional space with the euclidean distance $\|(x,y)\| = \sqrt{x^2+y^2}$ as the norm.When these spaces are described in terms of functions $f:S\to E$ (where $E = \Bbb{R}$ or $\Bbb{C}$), the set $S$ is just a set of $d$ elements, say $S = \{1,2,\ldots,d\}$. So an element of $l^2$ is a function $f$ from the set $\{1,2\}$ to $E$. If you write $f(1) = x$ and $f(2) = y$ then you can identify $f$ with $(x,y)$. In a finite-dimensional space, it may seem strange to think of points of the space as being functions. But in the case when $d = \infty$ it is natural to think of elements of $l^\infty$ as functions from the natural numbers to $E$.As I explained above, both $$l^2_1 ( \mathbb{R} )$$ and $$l^2_\infty ( \mathbb{R} )$$ are the space $\Bbb{R}^2$, but with different norms. For $l^2_1$, the norm is given by $\|(x,y)\|_1 = |x| + |y|$. For $l^2_\infty$, it is $\|(x,y)\|_\infty = \max\{|x|, |y|\}$.

In Example 11.5.7, the map $T:l^2_1 \to l^2_\infty$ is given by $T(x,y) = (x+y,x-y)$. The norm of $(x,y)$ in $l^2_1$ is $|x|+|y|$, and the norm of $T(x,y)$ in $l^2_\infty$ is $\max\{|x+y|,|x-y|\}$. Since those two expressions are equal, it follows that $T$ is an isometry.

Thanks so much Opalg ... a most helpful post indeed!

But just a clarification ...

You write:

" ... ... As I explained above, both $$l^2_1 ( \mathbb{R} )$$ and $$l^2_\infty ( \mathbb{R} )$$ are the space $\Bbb{R}^2$, but with different norms. For $l^2_1$, the norm is given by $\|(x,y)\|_1 = |x| + |y|$. For $l^2_\infty$, it is $\|(x,y)\|_\infty = \max\{|x|, |y|\}$. ... ... "I am slightly puzzled as to how you arrived at ... ... " ... For $l^2_\infty$, it is $\|(x,y)\|_\infty = \max\{|x|, |y|\}$ ... "I am trying to match your statement about $$\| . \|_\infty$$ with what Garling says about the norm $$\| . \|_\infty$$ ...In Section 11.2 on page 311 of Garling we read the following:" ... ... Arguing as in Proposition 11.1.11,

$$\| f \|_\infty = d_\infty ( f, 0 ) = \text{sup} \{ \| f(s) \|_\infty \ : \ s \in S \}$$

... ... ... ... ... "... and then going back to Proposition 11.1.11 we note that " ... ... $$d_\infty ( f, g ) = \text{sup} \{ d( f(s) , g(s) ) \ : \ s \in S \}$$ ... ... "Can you please explain how/why $$\| f \|_\infty$$ becomes $$\max\{|x|, |y|\}$$ ... I am guessing it has to do with "identifying" $$f$$ with $$(x,y)$$ ... and given that there are only two values sup becomes max ... but not sure ...

Hope you can help ... Just by the way I can see how it helps and why it is plausible to "identify" $$f$$ with $$(x,y)$$ ... but is this rigorous ... and logically/analytically the case .( that is true ... ) ... can you comment ... ?Peter

 

[Opalg]

In Section 11.2 on page 311 of Garling we read the following:

" ... ... Arguing as in Proposition 11.1.11,
$$\| f \|_\infty = d_\infty ( f, 0 ) = \text{sup} \{ \| f(s) \|_\infty \ : \ s \in S \}$$
... ... ... ... ... "

... and then going back to Proposition 11.1.11 we note that

" ... ... $$d_\infty ( f, g ) = \text{sup} \{ d( f(s) , g(s) ) \ : \ s \in S \}$$ ... ... "

Can you please explain how/why $$\| f \|_\infty$$ becomes $$\max\{|x|, |y|\}$$ ...

Formally and rigorously, an element of $$l^2_\infty ( \mathbb{R} )$$ is a function $f:S\to\Bbb{R}$, where $S = \{1,2\}$. The norm of $f$ is $\|f\|_\infty = \sup\{|f(s)|:s\in S\} = \max\{|f(1)|,|f(2)|\}$ (because the sup of a finite set of real numbers is just the maximum of its elements). If $f(1) = x$ and $f(2) = y$ then this becomes $\|f\|_\infty = \max\{|x|,|y|\}$.

Since the function $f$ is completely specified by its two values $f(1)$ and $f(2)$, it is convenient to identify $f$ with the ordered pair $(x,y)$.

 

[Math Amateur]

Formally and rigorously, an element of $$l^2_\infty ( \mathbb{R} )$$ is a function $f:S\to\Bbb{R}$, where $S = \{1,2\}$. The norm of $f$ is $\|f\|_\infty = \sup\{|f(s)|:s\in S\} = \max\{|f(1)|,|f(2)|\}$ (because the sup of a finite set of real numbers is just the maximum of its elements). If $f(1) = x$ and $f(2) = y$ then this becomes $\|f\|_\infty = \max\{|x|,|y|\}$.

Since the function $f$ is completely specified by its two values $f(1)$ and $f(2)$, it is convenient to identify $f$ with the ordered pair $(x,y)$.

Thanks for all your guidance on the above issues/problems ...

Your help and assistance is much appreciated ...

Peter