- #1
LCSphysicist
- 646
- 162
- TL;DR Summary
- I am having trouble to understand the reasoning that the author follows in these pages.
A rotation about an unit norm axis in R3can be given by the following, that gives basically the elements of the matrix of the rotation: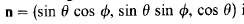
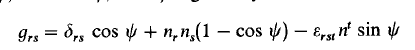
With these expression, we can obtain the three infinesimal rotations that corresponds to the three euler angles by first writing the three individuals matrix of these rotations, and then, taking the derivative:

Now, the autor gives the algebra regardind these transformations and talk about its representation in Rn

It is said that the representation A have the same algebra that g. And so he starts to talk about the canonical basis to represent as a way to write the representations.

After that, he returns to the beginning and says that

The relatios six and seven he says is that:
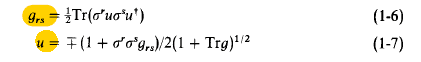
Now, i am extremelly confused about all this thing. More preciselly, i can't understand how 1.29 was obtained. It was used the A representation? How do he uses it? There is something to do with the canonical basis?