- #1
Natasha1
- 493
- 9
The converse of the Upper Bound Theorem would state that a graph which satisfies the inequality
[tex]e \leq { \frac{n (v-2)}{n-2} [/tex] is planar.
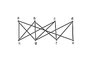
This converse is not true as seen in picture.
Verify that the inequality [tex]e \leq { \frac{n (v-2)}{n-2} [/tex] is true for this graph.
Using the inside-outside algorithm to show that the graph is actually non-planar.
[tex]e \leq { \frac{n (v-2)}{n-2} [/tex] is planar.
This converse is not true as seen in picture.
Verify that the inequality [tex]e \leq { \frac{n (v-2)}{n-2} [/tex] is true for this graph.
Using the inside-outside algorithm to show that the graph is actually non-planar.
Attachments
Last edited: