Upward Acceleration of a Hanging Mass Connected to Another By a Pulley

[Becca93]

Homework Statement
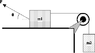
A 26.3 kg block (m1) is on a horizontal surface, connected to a 7.10 kg block (m2) by a massless string as shown in the figure below. The frictionless pulley has a radius R = 0.060 m and a moment of inertia I=0.090 kgm2. A force F = 220.1 N acts on m1 at an angle theta = 29.5°. There is no friction between m1 and the surface. What is the upward acceleration of m2?

Image attached.



The attempt at a solution

I'm got myself into a bit of circular thinking here.

T2 = m2a = m2(g + a)
a = alpha/r
alpha = τ/I
τ = T1rsinθ
T1 = Fparallel - m1a

I'm looking for the linear acceleration of the system, so I tried

T2 + T1 + m1a = Fpara
m2a + Ia + m1a = Fpara
a(m2 + I + m1a) = Fpara
a = Fpara / (m2 + I + m1)

a = 191.6 / (7.1 + .09 + 26.3)
a = 5.59 m/s

This isn't right. I'm not confident in the entire process - radius should be important and the way I have it, it isn't being taken into account. Problem is, I don't know how to work it in. I really need some guidance. Any help is appreciated!

 

[I like Serena]

Hi Becca93!

I'm a bit confused by the symbols you use.
It seems they are not quite consistent.
In particular the use of a, alpha, and g.
I'm sure that you mixed up a and alpha in at least one case, making you lose the radius r.

Furthermore there are effectively 2 external forces: Fpara and gravity on m₂.
I seem to be missing m₂g in your equations.

 

[Becca93]

Hi Becca93!

I'm a bit confused by the symbols you use.
It seems they are not quite consistent.
In particular the use of a, alpha, and g.
I'm sure that you mixed up a and alpha in at least one case, making you lose the radius r.

Furthermore there are effectively 2 external forces: Fpara and gravity on m₂.
I seem to be missing m₂g in your equations.

I worked it through with the guy that runs the math help center. To be honest, even I'm confused by my own workings.

But as for symbols, I use alpha for angular acceleration, a for linear acceleration, and g for acceleration due to gravity.

I think I need to start this question over from scratch, but I really have no clue where to begin to solve it. I'm trying to go through problems in prep for my final, but this is seriously not heartening.

 

[I like Serena]

You seem to be on the right track.
There's just a few ambiguities and (resulting) mistakes along the way.

So let's just start by your first equality:
T2 = m2a = m2(g + a)
How can it have "a" twice in it?

 

[Becca93]

You seem to be on the right track.
There's just a few ambiguities and (resulting) mistakes along the track.

So let's just start by your first equality:
T2 = m2a = m2(g + a)
How can it have "a" twice in it?

Shouldn't T2 be equal to m2's weight plus the effect the acceleration of the system has on it?

It doesn't make sense to me for it to be only the weight of gravity since the system is accelerating left.

 

[I like Serena]

Shouldn't T2 be equal to m2's weight plus the effect the acceleration of the system has on it?

Yes.

It doesn't make sense to me for it to be only the weight of gravity since the system is accelerating left.

No it doesn't. ;)

So where did T₂=m₂a come from?To state it more clearly, it works like this:
There are 2 forces on m₂: gravity and T₂.
The resulting force is their difference: T₂ - m₂g.
So according to Newton's 2nd law (F_resultant=ma), it follows that:

T₂-m₂g=m₂a.

This is the equation that you should have as far as I'm concerned.
Of course, it's just what you already said.
I just hope it makes things clearer.

 

[Becca93]

Yes.



No it doesn't. ;)

So where did T₂=m₂a come from?


To state it more clearly, it works like this:
There are 2 forces on m₂: gravity and T₂.
The resulting force is their difference: T₂ - m₂g.
So according to Newton's 2nd law (F_resultant=ma), it follows that:

T₂-m₂g=m₂a.



This is the equation that you should have as far as I'm concerned.
Of course, it's just what you already said.
I just hope it makes things clearer.

Yes, that does make sense.

Where else did I go wrong here?

 

[I like Serena]

Next is:
τ = T1rsinθ

This is not the proper torque.

On one side we have a tension T1 and on the other side T2.
So we've "lost" their difference, due to a reaction force from the pulley.
So what do you think the resulting torque on the pulley should be?

 

[Becca93]

Next is:
τ = T1rsinθ

This is not the proper torque.

On one side we have a tension T1 and on the other side T2.
So we've "lost" their difference, due to a reaction force from the pulley.
So what do you think the resulting torque on the pulley should be?

Would it be τ = (T1-T1)rsinθ then? What else is wrong?

 

[I like Serena]

Would it be τ = (T1-T1)rsinθ then? What else is wrong?

Why would there be a sine in there?
There shouldn't.

Btw, I'm off to bed now.
It's already very late where I live. :zzz:

For now, I'll give you one more hint.
You used "Ia" in your formula, but "I" would never be multiplied with the linear acceleration a.
What you should use is the torque formula with angular acceleration alpha.

Beyond that, I recommend that you set up the force and torque equations properly for m1, m2, and the pulley, and try to solve the problem again from there.

 

[Becca93]

Why would there be a sine in there?
There shouldn't.

Btw, I'm off to bed now.
It's already very late where I live. :zzz:

For now, I'll give you one more hint.
You used "Ia" in your formula, but "I" would never be multiplied with the linear acceleration a.
What you should use is the torque formula with angular acceleration alpha.

Beyond that, I recommend that you set up the force and torque equations properly for m1, m2, and the pulley, and try to solve the problem again from there.

I have no idea. I'll try to work this out in the morning. It's getting pretty late here too. Goodnight!

Thank for the advice. I'll take that into account when I try again.