erobz said:
What changes can we expect to see in the general behavior of that basic solution curve I presented in doing that?
The linearly damped harmonic oscillator is a well studied differential equation that one would encounter in a first semester course on differential equations. It is a linear, homogenous, second order differential equation. For such equations, you get nice analytical solutions in terms of sines, cosines and exponentials. [By contrast, with quadratic drag, the differential equation is no longer "linear"]
Underdamped, you get a sine wave within an exponentially decaying envelope.
Overdamped, you get a decaying exponential (technically, a sum of two)
Critically damped, you get a decaying exponential.
If the characteristic equation (a quadratic in this case) for the differential equation has two real roots, you get overdamping. If the characteristic equation has two complex roots (which will be conjugates), you get underdamping. If the equation has a single, repeated real root, you get critical damping.
In automobile shock absorbers, one normally designs for critical damping. The diagnostic test is to push down on the car's bumper, then release and see whether the car oscillates or smoothly returns to normal with no oscillation. If it bounces up and then back down, that is underdamping. The shocks are worn and need to be replaced. [This worked for the typical shocks that I grew up with -- linear valve strategies. It seems that much more complex strategies are available these days].
I've never looked much at pure quadratic damping. Intuitively, I'd expect that since the drag drops away dramatically near zero velocity that there is no possibility of overdamping, that a small oscillation will always exist and may be long-lived. I'd expect convergence to an ever-more-slowly decaying sine wave.
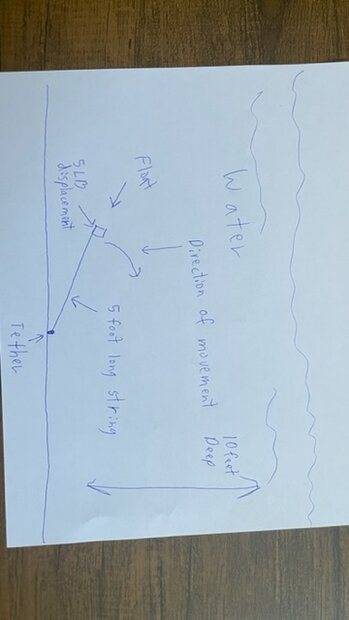 10 feet deep. The float is tethered to the bottom of the pool via a string that is pulled tight lengthwise and so is also laying on the bottom of the pool. The string is 4 feet long. If the float is released the float must travel in an arch because of the string tether. What equation do I use to figure out the resulting upward force of the float if it is traveling in an arch?
10 feet deep. The float is tethered to the bottom of the pool via a string that is pulled tight lengthwise and so is also laying on the bottom of the pool. The string is 4 feet long. If the float is released the float must travel in an arch because of the string tether. What equation do I use to figure out the resulting upward force of the float if it is traveling in an arch?