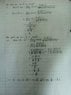Use Cauchy Residue Theorem to find the integral

Click For Summary
The discussion centers on using the Cauchy Residue Theorem to evaluate the integral ∫^{2∏}_{0} (cosθ)/(13+12cosθ) and demonstrate that it equals -4∏/15. A participant expresses confusion over their solution, which differs from the expected result, and questions where their error lies. They note a discrepancy in their factorization of a polynomial, indicating a potential mistake in their calculations. The conversation highlights the importance of accurate substitution and polynomial manipulation in applying the theorem correctly. Clarifying these steps is essential for reaching the correct integral value.
DanniHuang
Messages
6
Reaction score
0

Homework Statement



To find the integral by Cauchy Residue Theorem and apply substitution method.

Homework Equations



To show: ∫^{2∏}_{0}\frac{cosθ}{13+12cosθ}=-\frac{4∏}{15}

The Attempt at a Solution


The solution I have done is attached. It is different as what the question wants me to show. I do not know where I did it wrong.
 

Attachments

  • IMG_7273.jpg
    IMG_7273.jpg
    45.3 KB · Views: 1,262
  • IMG_7275.jpg
    IMG_7275.jpg
    23.9 KB · Views: 418
Physics news on Phys.org
Otherwise it looks fine to me, except that
6z^3+13z^2+6z = 6 z(z+2/3)(z+3/2) \neq z(z+2/3)(z+3/2)
 

Thread 'Distance between a Clock's hands when the distance is increasing most rapidly'

Question: A clock's minute hand has length 4 and its hour hand has length 3. What is the distance between the tips at the moment when it is increasing most rapidly?(Putnam Exam Question) Answer: Making assumption that both the hands moves at constant angular velocities, the answer is ## \sqrt{7} .## But don't you think this assumption is somewhat doubtful and wrong?
View full post »

Similar threads

Can I Use Substitution to Prove the Residue Theorem Integral?
  • · Replies 5 ·
Replies
5
Views
1K
Complex Integration Along Given Path
  • · Replies 3 ·
Replies
3
Views
2K
Calculating Integral Using Residue Theorem & Complex Variables
  • · Replies 4 ·
Replies
4
Views
2K
Graduate Cauchy’s integral theorem and residue theorem, what’s the difference
  • · Replies 1 ·
Replies
1
Views
2K
Find the residues of the following function + Cauchy Residue
  • · Replies 2 ·
Replies
2
Views
1K
Solving Complex Integrals with Cauchy's & Residue Theorem
  • · Replies 5 ·
Replies
5
Views
2K
Compute the residue of a function
  • · Replies 2 ·
Replies
2
Views
2K
How Do You Solve a Complex Integral Using Cauchy-Goursat's Theorem?
  • · Replies 32 ·
2
Replies
32
Views
3K
Complex Integration using residue theorem
  • · Replies 1 ·
Replies
1
Views
2K
Residue Theorem with real zero
  • · Replies 1 ·
Replies
1
Views
1K