Use Graph To Investigate Limit

[nycmathguy]

Homework Statement

Graphs and Limits

Relevant Equations

Piecewise Functions

For questions 24 and 26, Use the graph to investigate limit of f(x) as x→c. If the limit does not exist, explain why.

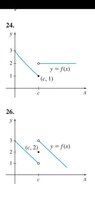
Question 24

For (a), the limit is 1.

For (b), the limit is cannot be determined due to the hole at (c, 2).

For (c), LHL does not = RHL.

I conclude the limit does not exist.

You say?

Question 26

For (a), the limit is 2.

For (b), the limit cannot be determined due to the hole at (c, 3).

For (c), LHL does not = RHL.

I conclude the limit does not exist.

You say?

 

[Mark44]

You say?

Did you forget to post the graph for these questions?
Also, just because there is a hole in the graph doesn't mean that a limit doesn't exist.

 

[nycmathguy]

Did you forget to post the graph for these questions?
Also, just because there is a hole in the graph doesn't mean that a limit doesn't exist.

Picture has been added.

 

[Mark44]

Ques. 24

For (b), the limit is cannot be determined due to the hole at (c, 2).

No, this is incorrect. The presence or absence of a hole doesn't affect the limit.
As x approaches c from the right, what are the function values doing?

I conclude the limit does not exist.

This is the correct conclusion, but you've based it on faulty reasoning.

Ques. 26

For (a), the limit is 2.

For (b), the limit cannot be determined due to the hole at (c, 3).

No to both. As x approaches c from the left, what value are the function values approaching? The fact that the point (c, 2) is on the graph has nothing to do with what the limit might be.
As x approaches c from the right, what are the function values doing, again ignoring the point at (c, 2)?

I conclude the limit does not exist.

Correct conclusion but based on faulty reasoning.

 

[nycmathguy]

Ques. 24No, this is incorrect. The presence or absence of a hole doesn't affect the limit.
As x approaches c from the right, what are the function values doing?

This is the correct conclusion, but you've based it on faulty reasoning.

Ques. 26No to both. As x approaches c from the left, what value are the function values approaching? The fact that the point (c, 2) is on the graph has nothing to do with what the limit might be.
As x approaches c from the right, what are the function values doing, again ignoring the point at (c, 2)?

Correct conclusion but based on faulty reasoning.

Let me reply to yours one at a time from top to bottom.

1. As x tends to c from the right, f(x) goes to a height of 2.

2. Let me try 26 again.

As x tends to c from the left, f(x) goes to a height of 1.

As x tends to c from the right, f(x) goes to a height of 3.

Since the LHL does = THE RHL, the limit for f(x) does not exist.

You now say?

 

[Mark44]

They're all fine now.

 

[nycmathguy]

They're all fine now.

This makes me feel better. I am slowly getting this limits stuff. I also know that limits is calculus 3 is very different. I am ok so far in the textbook.