Use method of difference to find sum of series

[chwala]

Homework Statement

see attached.

Relevant Equations

series sum

My interest is on the (highlighted part in yellow ) of finding the partial fractions- Phew took me time to figure out this out

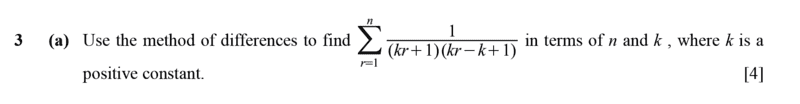
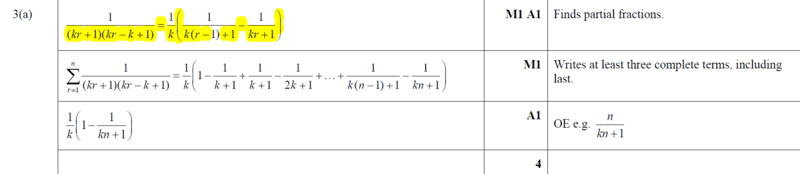
My approach on the highlighted part;

i let

$(kr+1) =x$

then, $\dfrac{1}{(kr+1)(kr-k+1)} = \dfrac{1}{x(x-k)}$
then,

$\dfrac{1}{(x)(x-k)}=\dfrac{A}{x} +\dfrac{B}{x-k}$

$1=A(x-k)+Bx$

$Ax+Bx=0$
$-Ak=1$

$A=\dfrac{-1}{k}$

i know that $A+B=0$
$B=\dfrac{1}{k}$

thus,

$\dfrac{1}{(x)(x-k)}=\dfrac{-1}{kx} +\dfrac{1}{k(x-k)}$

$\dfrac{1}{(kr+1)(kr-k+1)}=\dfrac{-1}{k(kr+1)} +\dfrac{1}{k(kr-k+1)}$

$\dfrac{1}{(kr+1)(kr-k+1)}= \dfrac{1}{k(kr-k+1)}-\dfrac{1}{k(kr+1)}$

$\dfrac{1}{(kr+1)(kr-k+1)}= \dfrac{1}{k(k(r-1)+1)}-\dfrac{1}{k(kr+1)}$

any simpler or alternative approach (in determining the partial fractions) prompted this post.

 

[chwala]

This is also related,

solution:

My steps,

$\lim_{n \rightarrow +\infty} \left[\dfrac{n}{kn+1}\right] = \lim_{n \rightarrow +\infty} \left[\dfrac{1}{k+1/n}\right]= \left[\dfrac{1}{k+0}\right]=\dfrac{1}{k}$