- #1
Celer
- 13
- 0
Using a simple pendulum to determine "g"
1. Using a simple pendulum to determine "g"
Basically, we were asked to do an experiment where we measured with a stopwatch for 20 complete oscillations for a pendulum bob swinging through a small arc (10 degrees). We increased the length of the string attached to the bob by 10 cm every time from 20cm to 1m.
Then, we were supposed to graph length to time^2 and figure out a value of "g" and give a straight line graph in the form of y=mx + c
Basically, i recorded data like this
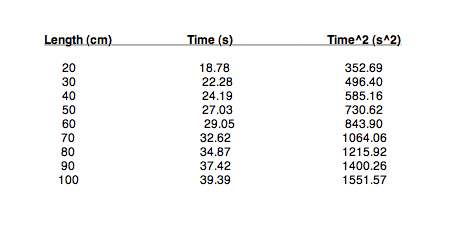
Using Time^2, and Length, I plot the graph and drew a line of best fit in the form of y=mx + c. I got a slope (m) of 14.371
I used g = 4pi^2 / m
Where m is the slope of the graph.
Using the above equation, I subbed in all the numbers to find "g" for the first point of data.
So, g = 4pi^2/14.371
g = 2.747
My question is, as we all know "g" should be 9.8 meters per second ^2. I am getting a figure of 2.747 meters per second ^2. Which is awfully off what it should be right?
I am wondering if one of my equations are set up wrong, or did I measure something wrong?
1. Using a simple pendulum to determine "g"
Basically, we were asked to do an experiment where we measured with a stopwatch for 20 complete oscillations for a pendulum bob swinging through a small arc (10 degrees). We increased the length of the string attached to the bob by 10 cm every time from 20cm to 1m.
Then, we were supposed to graph length to time^2 and figure out a value of "g" and give a straight line graph in the form of y=mx + c
Basically, i recorded data like this
Using Time^2, and Length, I plot the graph and drew a line of best fit in the form of y=mx + c. I got a slope (m) of 14.371
Homework Equations
I used g = 4pi^2 / m
Where m is the slope of the graph.
The Attempt at a Solution
Using the above equation, I subbed in all the numbers to find "g" for the first point of data.
So, g = 4pi^2/14.371
g = 2.747
My question is, as we all know "g" should be 9.8 meters per second ^2. I am getting a figure of 2.747 meters per second ^2. Which is awfully off what it should be right?
I am wondering if one of my equations are set up wrong, or did I measure something wrong?