Using conservation of energy and momentum in projectile motion

[MatinSAR]

Homework Statement

A projectile is fired at an angle of 45° with initial kinetic energy $E_0$. At the top of its trajectory, the projectile explodes with additional energy $E_0$ into two fragments. One fragment of mass $m_1$ travels straight down. What is the velocity (magnitude and direction) of the second fragment of mass $m_2$ and the velocity of the first? What is the ratio of $m_1/m_2$ when $m_1$ is a maximum?

Relevant Equations

Conservation of energy and momentum.

I am going to use this coordinate system:

According to the answer of the book, I think no force is acting on this projectile:

Let's say at top of it's trajectory its velocity is $u$.

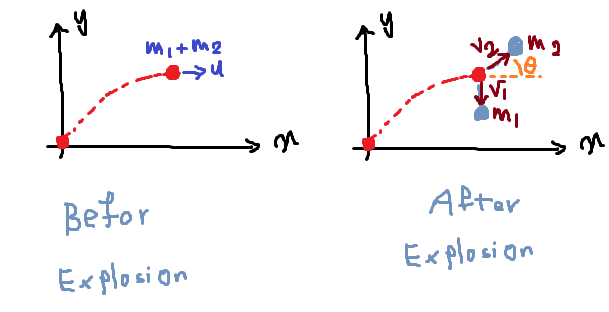
Conservation of energy : $$2E_0=\frac 1 2 m_1 v_1^2+\frac 1 2 m_2 v_2^2$$
Conservation of momentum in x-direction: $$ (m_1+m_2)u = m_2v_2 \cos \theta $$
Conservation of momentum in y-direction: $$ m_2v_2 \sin \theta = m_1 v_1$$

I should find $v_1$ and $v_2$ and $\theta$. But I failed. Are my equations wrong? Any help would be appreciated.

 

[kuruman]

Gravity is an external force acting on the projectile in the vertical direction.

 

[MatinSAR]

Gravity is an external force acting on the projectile in the vertical direction.

Why doesn’t the answer in the book mention potential due to gravity in the energy conservation formula?
And why it has written conservation of momentum for vertical direction (z-direction) when gravity exists!

 

[kuruman]

Energy is not conserved because there is an explosion which releases additional mechanical energy. You see that in what you call the energy conservation equation. It says that the total kinetic energy of the fragments immediately after the explosion is twice the kinetic energy of the projectile immediately before the explosion. Do you see why that is? You may assume that the explosion occurs so fast that the potential energy of the center of mass does not change appreciably.

 

[MatinSAR]

Do you see why that is?

Yes.

Energy is not conserved

I know that mechanical energy is not conserved. But I guess total energy is conserved :$$E_i+E_{explosion}=E_f$$ I just can't see why the book wrote momentum conservation in vertical direction. Because as you've mentioned gravity exist ...

 

[Mister T]

Why doesn’t the answer in the book mention potential due to gravity in the energy conservation formula?

Because it's not relevant. The explosion occurs so quickly that the change in gravitational potential energy is negligible.

And why it has written conservation of momentum for vertical direction (z-direction) when gravity exists!

The force exerted on the projectile fragments during the explosion is so large that the force of gravity is negligible.

 

[MatinSAR]

Because it's not relevant. The explosion occurs so quickly that the change in gravitational potential energy is negligible.

I think I've just found my mistake in this part.

The force exerted on the projectile fragments during the explosion is so large that the force of gravity is negligible.

Shouldn’t this information have been included in the question? How could I have guessed …
So, in the questions of projectile explosion, can the momentum be assumed to be conserved even in vertical direction? With knowing that the force of gravity is negligible.

 

[kuruman]

Shouldn’t this information have been included in the question? How could I have guessed …

Perhaps, but once you've seen it you know to use it next time. It's no different from the assumption you have to make in the case of a ballistic pendulum that the bullet embeds itself instantaneously and the bullet + block system starts moving from rest. After all, a completely inelastic collision is an explosion with time running backwards. This simplifying assumption of instantaneous energy release (or absorption) makes the problem doable using what is given. Without it, you will need more details.

 

[MatinSAR]

Perhaps, but once you've seen it you know to use it next time. It's no different from the assumption you have to make in the case of a ballistic pendulum that the bullet embeds itself instantaneously and the bullet + block system starts moving from rest. After all, a completely inelastic collision is an explosion with time running backwards. This simplifying assumption of instantaneous energy release (or absorption) makes the problem doable using what is given. Without it, you will need more details.

Everything is clear now.


@kuruman and @Mister T
Thanks for your time.

 

[Mister T]

Shouldn’t this information have been included in the question?

Not typically, no. Read the beginning of the chapter or section where conservation of momentum or collisions is first discussed. There you should find a "disclaimer" that in a collision the forces exerted on the objects by each other are considered to be so large that all other forces can be ignored. I realize that this is an explosion, but explosions are treated as collisions in reverse.

 

[MatinSAR]

Not typically, no. Read the beginning of the chapter or section where conservation of momentum or collisions is first discussed. There you should find a "disclaimer" that in a collision the forces exerted on the objects by each other are considered to be so large that all other forces can be ignored. I realize that this is an explosion, but explosions are treated as collisions in reverse.

That makes sense. Thanks for your help.


In a lecture note from my university professor, I discovered an alternative way to explain this concept. Let’s consider our system as comprising the projectile and the Earth so there is no net external force acting on the object. So system's momentum is conserved. And the change in Earth’s momentum due to the explosion is negligible.

I think this is similar to what was suggested above. Anyway, both methods yield the same result.

 

[Mister T]

Let’s consider our system as comprising the projectile and the Earth so there is no net external force acting on the object.

On the system.

So system's momentum is conserved. And the change in Earth’s momentum due to the explosion is negligible.

I think this is similar to what was suggested above. Anyway, both methods yield the same result.

Yes, they are probably equivalent approximations.

 

[MatinSAR]

On the system.

Yes. The problem was with my translation. Thanks for pointing out ...

 

[haruspex]

Shouldn’t this information have been included in the question? How could I have guessed

Unless there is information to the contrary, sudden impacts are taken to be of arbitrarily short duration. Generally, you can know what the change in momentum is without knowing the force profile (how it varies over time).
If the force profile is $F(t)$ for period $\Delta t$ then $\Delta p=\int_t^{t+\Delta t} F.dt$.

My mantra wrt idealisations is that the safe approach is to start with a realistic model then take the limit as the idealisation is approached. One case that trips people (including teachers) up is impulsive friction. Suppose a ball rolls on horizontal ground into a vertical wall and bounces back. Does friction matter?
Between ball and ground, no. Because the normal force never exceeds mg, the impulse from ground friction is at most $\mu mg\Delta t$ which vanishes as $\Delta t\rightarrow 0$.
But between ball and wall, if the net horizontal impulse from the wall is $p$ then the vertical frictional force can be $\mu p$, which does not vanish. It follows that the ball must become airborne if $\mu_k>0$.
If the angle between ground and wall is acute then it gets really interesting.

 

[MatinSAR]

Unless there is information to the contrary, sudden impacts are taken to be of arbitrarily short duration. Generally, you can know what the change in momentum is without knowing the force profile (how it varies over time).
If the force profile is $F(t)$ for period $\Delta t$ then $\Delta p=\int_t^{t+\Delta t} F.dt$.

My mantra wrt idealisations is that the safe approach is to start with a realistic model then take the limit as the idealisation is approached. One case that trips people (including teachers) up is impulsive friction. Suppose a ball rolls on horizontal ground into a vertical wall and bounces back. Does friction matter?
Between ball and ground, no. Because the normal force never exceeds mg, the impulse from ground friction is at most $\mu mg\Delta t$ which vanishes as $\Delta t\rightarrow 0$.
But between ball and wall, if the net horizontal impulse from the wall is $p$ then the vertical frictional force can be $\mu p$, which does not vanish. It follows that the ball must become airborne if $\mu_k>0$.
If the angle between ground and wall is acute then it gets really interesting.

Thank you for your help @haruspex ...

If the angle between ground and wall is acute then it gets really interesting.

Do you mean something like this?

 

[haruspex]

Do you mean something like this?
View attachment 344175

Yes

 

[MatinSAR]

Yes

Ok. I will think more on this after my exam. Right now I can't think of a reason for :

If the angle between ground and wall is acute then it gets really interesting.

 

[haruspex]

Ok. I will think more on this after my exam. Right now I can't think of a reason for :

Because the the rebound from the wall will tend to push the ball down, creating an impulse from the ground.

 

[MatinSAR]

Because the the rebound from the wall will tend to push the ball down, creating an impulse from the ground.

I understand. Interesting! Thanks for your help @haruspex