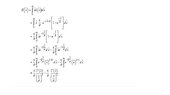Using gamma function to solve an integral

[mathjam0990]

Hello,

I have attached a picture of the integral I am solving. I understand at the end how they turned the function (in the second to last step) into gamma(2) BUT what I do not understand is how you can simply just remove the (2/theta) out of the exponent of e, turn it into gamma(2) then divide it by (2/theta)^2 in that last step. Based on the fact that gamma(a) = integral of [ya-1 * e-y]dy I see for this particular example in question that the (2/theta) is out of place (so to say) if we are trying to get our integral to take the form of the integral equaling gamma(a). So, with all that being said, how can we simply just take that (2/theta) out of the exponent of e, turn the whole thing into a gamma and then just divide by (2/theta)^2 ?? Is there a trick or something I am overlooking? Please help me if you can!

Thank you!

 

[alyafey22]

Let us solve

$$\int^\infty_0 e^{-\frac{2x}{\theta}}x \,dx $$

Let $t = \frac{2x}{\theta}$ which implies that $dx = \frac{\theta}{2}dt$

$$\int^\infty_0 e^{-t}\times \frac{\theta}{2}t \times \frac{\theta}{2} \,dt = \frac{\theta^2}{4}\int^\infty_0t e^{-t}\,dt$$

Then use the definition of the gamma function

 

[mathjam0990]

Thank you ZaidAlyafey!