Using integration find the volume of cutted cone

[Amer]

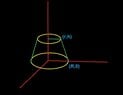
if we cut a right cone parallel to the base having a two radius r and R The picture
View attachment 407

I want to use the volume of revolution around the y-axis
we have the line

y - 0 = \dfrac{h}{r-R} (x - R)
x = \frac{r-R}{h} y +R

The volume will be
\pi \int_{0}^{h} \left(\frac{r-R}{h} y + R\right)^2 dy
\pi \int_{0}^{h} \frac{(r-R)^2y^2}{h^2} + \frac{2R(r-R)y}{h} + R^2 dy
now i just have to evaluate the integral, did i miss something ?

 

[MarkFL]

Looks correct to me, however, I would use a substitution to simplify matters:

$\displaystyle V=\pi\int_0^h\left(\frac{r-R}{h}y+R \right)^2\,dy$

Let:

$\displaystyle u=\frac{r-R}{h}y+R\,\therefore\,du=\frac{r-R}{h}\,dy$

hence:

$\displaystyle V=\frac{h}{r-R}\pi\int_{R}^{r}u^2\,du$