- #1
FireStorm000
- 169
- 0
Using Magnetic Fields in Place of Heat Shielding
Joshua “FireStorm” King
Note: All Graphs are in SI base units
Note 2: I strongly recommend downloading the document version of this post as the equations are actually readable there.
RTF Format:View attachment FireStorm-Magnetic Heat Shielding.rtf.zip
Docx Format:View attachment FireStorm-Magnetic Heat Shielding.docx.zip
Introduction: The Problem
I'm a real space geek; when I was sitting in my AP physics class learning about magnetic fields, I thought "Why not use magnetic fields instead of bulky one-use heat shields." I mean, let’s face it: heat shields kind of suck; they are external to the spacecraft , and thus easily damaged by debris (See Columbia disaster). They also can really only be used once, which is fine in the case of a single use vehicle, but what about re-usable craft such as the shuttle, or any interplanetary craft we may build in the future.
Introduction: My Solution
In theory, magnetic fields should be just as effective as a hunk of metal or ceramic; maybe even more so. When a charged particle (such as the protons and electrons in the plasma disassociated when a spacecraft reenters the atmosphere) encounters a magnetic field it encounters a force perpendicular to both the magnetic field and velocity. This causes the particle in question to follow a circular path. In other words, the magnetic field causes the particle to turn around (half circle) in some radius R. Once many particles start doing this they should start colliding with other incoming particles, creating dense zone of plasma where the pressure from the magnetic field turning particles around counters exactly the pressure of the onrushing plasma.
Uses
Aero Braking: spacecraft could use an effectively giant ‘magnetic sail’ so to speak to slow itself down in a planet’s exosphere; the atmosphere up there should already be ionized from solar radiation, thus one could easily form a sail with many thousands of times the cross section of the spacecraft .
Aero Capture: Similar to Aero Braking, Aero Capture attempts to slow the spacecraft down to orbital velocity in one pass. This can be a very hit or miss maneuver as it can be very difficult to calculate accurately. By varying the strength of the magnetic field as the spacecraft plunges into the atmosphere, one could control precisely the delta v that the spacecraft receives, and end up in a better orbit.
Reentry: Keeps the intensely hot plasma created during atmospheric reentry away from the relatively fragile spacecraft . No heat shield would be required (or at least much less shielding would be needed). Craft would be reusable, as there is nothing to ablate. The heat shield is the atmosphere. Also, aerodynamic considerations don’t need to be made for hypersonic flight, because the craft will be encased in a bubble of plasma. Once the craft slows down sufficiently, the air will stop ionizing, and the spacecraft can handle in atmosphere like a plane, or deploy parachutes, etc.
Derivations: how to find external B field, turning radius of particles
The turning radius of a given particle (assuming a roughly uniform magnetic field) is:
F=qvB
a_ctp=v^2 / r
F=ma
r=mv/qB
Remember that equation for a second
Now, knowing the magnetic field inside a superconducting magnet can easily reach 25T, we can use that number to calculate the B field outside the solenoid.
dB/dl = μ_0/4π I/x^2
B_(solenoid )= μ_0 nI
B_(ext )= B_(close wire) – B_(far wire)
B_ext =(2r)μ_0/4π In(( 1)/( x – r )^2 – 1/( x + r )^2 )
B_(ext )= r^2/π B_(sol ) ( 2x + r )〖( x + r )〗^(-2) 〖( x – r )〗^(-2)
Thus we now have an expression that will tell us the external magnetic field, for a solenoid of radius r, internal field strength Bsol at distance X. Graphing that with Bsol = 25T and r = 3m gives us:
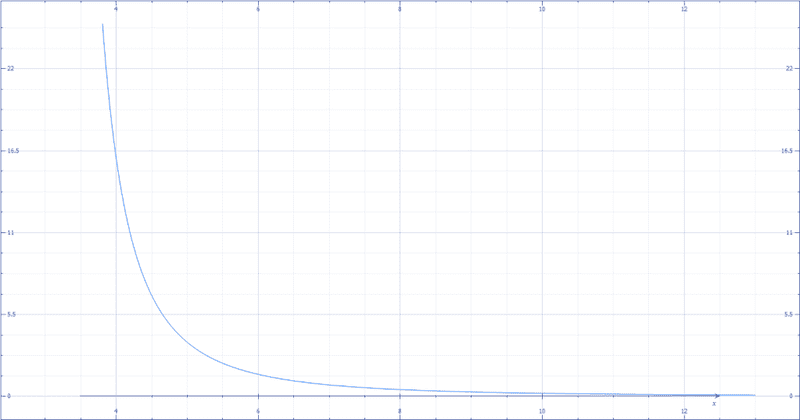
One can see that VERY significant magnetic fields would exist within several meters of the solenoid. A half Tesla magnetic field would exist 5 meters from the solenoid. Were the solenoid literally part of the exterior hull, that would mean that, at the hull(assume .25meters), we’d have a field of 278 Tesla. Let’s calculate the turning radius of a proton under those conditions:
r_turning=mv/(q 〖r_sol〗^2/π B_sol ( 2x + r_sol )〖(x+r_sol )〗^(-2) 〖( x–r_sol )〗^(-2) )
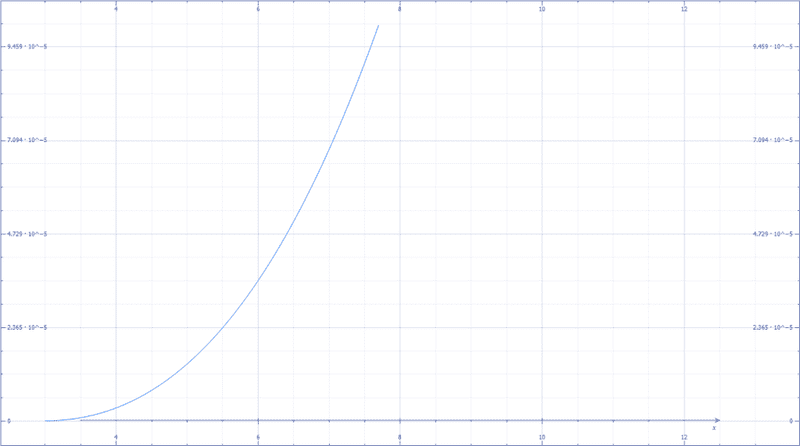
We can now further see that particles coming with 10m of the craft will have a turning radius on the order of .1 mm. 5 meters from the hull the turning radius of particles is .13mm.
Derivation: Conclusions
In my mind at least, this means that the magnetic field will end up pushing against the flow of charged particles, inducing drag much like a conventional heat shield. Based on the above calculations, even a modest strength solenoid would have an enormous effect on the plasma at anything above 1000m/s.
Questions
How practical is this? If there aren’t any glaring problems, why hasn’t it been used?
What shape would the “plasma bubble” take? Would one form, or would the plasma be more dispersed?
How effective is this as a heat shield? Does it protect the spacecraft completely?
What would the coefficient of drag be for varying angles of attack?
Given that particles spiral along magnetic field lines, what happens at the open ends of the solenoid?
What would be a good layout of electromagnets for stability, control, and redundancy on an actual craft?
Approaching the Answers
I definitely want to open this idea up to discussion. Pros and Cons, is my math right, etc. I would also like to find a good magneto hydrodynamic simulator that will let me see the effects of hypersonic plasma flow over the solenoid; I can vary the angle of attack of the solenoid(s) and see how protected the spacecraft would be. I think a simulator will be necessary to answer a majority of these questions to my satisfaction.
Joshua “FireStorm” King
Note: All Graphs are in SI base units
Note 2: I strongly recommend downloading the document version of this post as the equations are actually readable there.
RTF Format:View attachment FireStorm-Magnetic Heat Shielding.rtf.zip
Docx Format:View attachment FireStorm-Magnetic Heat Shielding.docx.zip
Introduction: The Problem
I'm a real space geek; when I was sitting in my AP physics class learning about magnetic fields, I thought "Why not use magnetic fields instead of bulky one-use heat shields." I mean, let’s face it: heat shields kind of suck; they are external to the spacecraft , and thus easily damaged by debris (See Columbia disaster). They also can really only be used once, which is fine in the case of a single use vehicle, but what about re-usable craft such as the shuttle, or any interplanetary craft we may build in the future.
Introduction: My Solution
In theory, magnetic fields should be just as effective as a hunk of metal or ceramic; maybe even more so. When a charged particle (such as the protons and electrons in the plasma disassociated when a spacecraft reenters the atmosphere) encounters a magnetic field it encounters a force perpendicular to both the magnetic field and velocity. This causes the particle in question to follow a circular path. In other words, the magnetic field causes the particle to turn around (half circle) in some radius R. Once many particles start doing this they should start colliding with other incoming particles, creating dense zone of plasma where the pressure from the magnetic field turning particles around counters exactly the pressure of the onrushing plasma.
Uses
Aero Braking: spacecraft could use an effectively giant ‘magnetic sail’ so to speak to slow itself down in a planet’s exosphere; the atmosphere up there should already be ionized from solar radiation, thus one could easily form a sail with many thousands of times the cross section of the spacecraft .
Aero Capture: Similar to Aero Braking, Aero Capture attempts to slow the spacecraft down to orbital velocity in one pass. This can be a very hit or miss maneuver as it can be very difficult to calculate accurately. By varying the strength of the magnetic field as the spacecraft plunges into the atmosphere, one could control precisely the delta v that the spacecraft receives, and end up in a better orbit.
Reentry: Keeps the intensely hot plasma created during atmospheric reentry away from the relatively fragile spacecraft . No heat shield would be required (or at least much less shielding would be needed). Craft would be reusable, as there is nothing to ablate. The heat shield is the atmosphere. Also, aerodynamic considerations don’t need to be made for hypersonic flight, because the craft will be encased in a bubble of plasma. Once the craft slows down sufficiently, the air will stop ionizing, and the spacecraft can handle in atmosphere like a plane, or deploy parachutes, etc.
Derivations: how to find external B field, turning radius of particles
The turning radius of a given particle (assuming a roughly uniform magnetic field) is:
F=qvB
a_ctp=v^2 / r
F=ma
r=mv/qB
Remember that equation for a second
Now, knowing the magnetic field inside a superconducting magnet can easily reach 25T, we can use that number to calculate the B field outside the solenoid.
dB/dl = μ_0/4π I/x^2
B_(solenoid )= μ_0 nI
B_(ext )= B_(close wire) – B_(far wire)
B_ext =(2r)μ_0/4π In(( 1)/( x – r )^2 – 1/( x + r )^2 )
B_(ext )= r^2/π B_(sol ) ( 2x + r )〖( x + r )〗^(-2) 〖( x – r )〗^(-2)
Thus we now have an expression that will tell us the external magnetic field, for a solenoid of radius r, internal field strength Bsol at distance X. Graphing that with Bsol = 25T and r = 3m gives us:
One can see that VERY significant magnetic fields would exist within several meters of the solenoid. A half Tesla magnetic field would exist 5 meters from the solenoid. Were the solenoid literally part of the exterior hull, that would mean that, at the hull(assume .25meters), we’d have a field of 278 Tesla. Let’s calculate the turning radius of a proton under those conditions:
r_turning=mv/(q 〖r_sol〗^2/π B_sol ( 2x + r_sol )〖(x+r_sol )〗^(-2) 〖( x–r_sol )〗^(-2) )
We can now further see that particles coming with 10m of the craft will have a turning radius on the order of .1 mm. 5 meters from the hull the turning radius of particles is .13mm.
Derivation: Conclusions
In my mind at least, this means that the magnetic field will end up pushing against the flow of charged particles, inducing drag much like a conventional heat shield. Based on the above calculations, even a modest strength solenoid would have an enormous effect on the plasma at anything above 1000m/s.
Questions
How practical is this? If there aren’t any glaring problems, why hasn’t it been used?
What shape would the “plasma bubble” take? Would one form, or would the plasma be more dispersed?
How effective is this as a heat shield? Does it protect the spacecraft completely?
What would the coefficient of drag be for varying angles of attack?
Given that particles spiral along magnetic field lines, what happens at the open ends of the solenoid?
What would be a good layout of electromagnets for stability, control, and redundancy on an actual craft?
Approaching the Answers
I definitely want to open this idea up to discussion. Pros and Cons, is my math right, etc. I would also like to find a good magneto hydrodynamic simulator that will let me see the effects of hypersonic plasma flow over the solenoid; I can vary the angle of attack of the solenoid(s) and see how protected the spacecraft would be. I think a simulator will be necessary to answer a majority of these questions to my satisfaction.
Last edited:
