user12323567
- 20
- 1
- Homework Statement
- Determine the force in members BC, HC, and HG. State if these members are in tension or compression.
- Relevant Equations
- Rigid-body assumption
Taking the moments about points A and C, why is a distance of 3 meters used in Fhc and Fhg? Isn’t it supposed to be 1.5 meters for both?
I acknowledge that Fhc and Fhg have x and y components, but were we considering the horizontal or vertical component (or both components) of either Fhc and Fhg in taking moments about points A and C respectively?


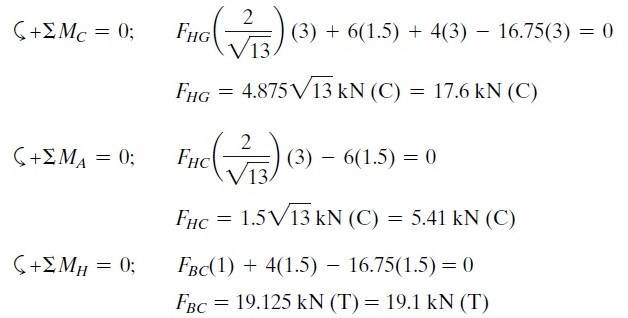
I acknowledge that Fhc and Fhg have x and y components, but were we considering the horizontal or vertical component (or both components) of either Fhc and Fhg in taking moments about points A and C respectively?