Using separation of variables in solving partial differential equations

[chwala]

Homework Statement

Kindly see attached;

Relevant Equations

separation of variables, in essence breaking down a pde into two ordinary differential equations.

I am reading on this part; and i realize that i get confused with the 'lettering' used... i will use my own approach because in that way i am able to work on the pde's at ease and most importantly i understand the concept on separation of variables and therefore would not want to keep on second guessing on the 'letters used' in the textbook notes ...as attached below;

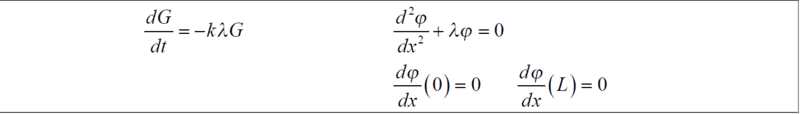
This is (my approach) steps to the working...
$U_t$= $k U_{xx}$
Let $U(x,t)$= $X(x) T(t)$
Therefore,
$XT^{'}$=$kX^{''}T$
$\frac{T^{'}}{kT}$=$\frac{X^{''}}{X}$=$-λ$
From here we have one initial condition,i.e $u(x,0)$=$f(x)$ and two spatial boundary conditions, i.e $u_x(0,t)=0$ and $u_x(L,t)=0$
Therefore using the Boundary conditions, we shall have,
$u_x$= $X'T$
$0$=$X'(0)T(t)$ and also, $0= X'(L)T(t)$
If $T(t)=0$, then we shall have a trivial solution and therefore for a non- trivial solution to be realized we need to have,
$X'(0)=0$ →$X'(L)=0$
and therefore our problem is reduced to,
$T'+λkT=0$ and $X^{''} + λX=0$
$U_x(0)=0$
$U_x(L)=0$
I intend to use this approach in problems related to pde...regards,

 

[chwala]

This was not a question, rather my way of handling the pde's ...the intention was to keep you informed on my way of solving future pde's on the forum. I guess it should not be regarded as unanswered thread...