Using virtual work to find the angle of a bar supported by two planes

[tomul]

Homework Statement

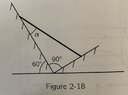
A uniform bar of length L and weight W is supported at its ends by two inclined planes as shown in the attached diagram. From the principle of virtual work, find the angle α at which the bar is in equilibrium. (Neglect friction)

Relevant Equations

For a system in equilibrium, the work done over a virtual displacement is zero:
ΣFd = 0

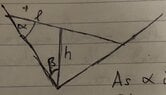
I imagined the bar slipping along a virtual displacement, with the top and the bottom slipping by equal amounts. Since the planes are orthogonal, I took the components of these displacements: the lower end is displaced Lsinα in the direction of the right plane and by Lcosα in the direction of the left plane. For the lower end I used the remaining angle in the triangle, 180-90-α = 90-α, giving components -Lsin(90-α)=-Lcosα and -Lcos(90-α)=-Lsinα. I then broke the bar into five points, one at its leftmost tip, one mid way between the centre and the leftmost tip, one at the centre, one mid way between the centre and the rightmost tip, and one at its rightmost tip. I assumed that the distance from the centre would be proportional to the fraction of the displacement of the tips which that point moves, so the center would have no displacement, and the two midpoints would have a displacement of components 1/2 Lcosα, 1/2 L sinα, -1/2Lcosα, and -Lsinα. Since the bar is uniform, both halfs of the bar can be thought of as having the weight acting from the two midpoints so the work done for each of the components would be W/2 L cosα, W/2 L sinα, -W/2 L cosα, and -W/2 Lsinα. Using the principle of virtual work, these should sum to zero:

W/2 L cosα + W/2 L sinα - W/2 L cosα - W/2 L sinα = 0

Dividing the equation by ( cosα W/2 L ) gives:

1 + tanα - 1 - tanα = 0
tan α = tan α
α = arctan(tan α)
α = α

Which is not exactly useful for finding α. What mistake did I make which brought me to this dead-end?

 

[ergospherical]

Since any displacement of either end of the rod is orthogonal to the normal contact force, the only force that does work on the rod is the weight $\mathbf{W}$.

Determine the height $h(\alpha)$ of the centre of mass of the rod as a function of $\alpha$. Because $\mathbf{W} = -W \hat{\mathbf{y}}$ acts through the centre of mass, the angle at which the weight force does no work when the angle increases by $d\alpha$ can then be deduced by setting $dh = 0$.

 

[haruspex]

the top and the bottom slipping by equal amounts

By the same linear distances? No.

the center would have no displacement

Think about the distance from the centre of the bar to the intersection of the planes. As the angle of the bar changes, what happens to that distance?

 

[tomul]

By the same linear distances? No.

Think about the distance from the centre of the bar to the intersection of the planes. As the angle of the bar changes, what happens to that distance?

It increases. Okay so I need to just consider this central displacement and the weight acting through it? Well I'm having trouble with that too which is in my reply to ergospherical...

Since any displacement of either end of the rod is orthogonal to the normal contact force, the only force that does work on the rod is the weight $\mathbf{W}$.

Determine the height $h(\alpha)$ of the centre of mass of the rod as a function of $\alpha$. Because $\mathbf{W} = -W \hat{\mathbf{y}}$ acts through the centre of mass, the angle at which the weight force does no work when the angle increases by $d\alpha$ can then be deduced by setting $dh = 0$.

Okay, I've applied the sine rule to find $h(\alpha)$

$\frac{sin\alpha}{h(\alpha)} = \frac{sin(90-\alpha)}{L/2}$
$\frac{sin\alpha}{h(\alpha)} = \frac{2 cos\alpha}{L}$
$h(\alpha) = \frac{L}{2} tan(\alpha)$

Considering a virtual displacement:
$\delta h = h(\alpha + \delta\alpha) = \frac{L}{2} tan(\alpha + \delta\alpha)$
Setting $\delta h = 0$ and therefore $\delta\alpha$=0:
$\frac{L}{2} tan(\alpha) = 0$
$tan(\alpha) = 0$
$\alpha = 0$

which isn't right

 

[haruspex]

It increases.

Is that just a guess? Apply some geometry.

 

[tomul]

Is that just a guess? Apply some geometry.

Okay, applying the sine rule:
$\frac{sin\alpha}{h} = \frac{sin\beta}{l}$
$h = \frac{l sin\alpha}{sin\beta}$

Since $\alpha$ < 90 deg, $sin\alpha$ increases with $\alpha$, and since $sine\alpha$ is proportional to $h$, $h$ will increase.

The only problem with this is if $l$ or $\beta$ change with $\alpha$ but I honestly can't think of a geometric reason why they should or shouldn't...

 

[haruspex]

Okay, applying the sine rule:
$\frac{sin\alpha}{h} = \frac{sin\beta}{l}$
$h = \frac{l sin\alpha}{sin\beta}$

Since $\alpha$ < 90 deg, $sin\alpha$ increases with $\alpha$, and since $sine\alpha$ is proportional to $h$, $h$ will increase.

The only problem with this is if $l$ or $\beta$ change with $\alpha$ but I honestly can't think of a geometric reason why they should or shouldn't...

You do not need any trig, just basic geometry.
What do you know about the diameter of the circumcircle of a right angled triangle?

 

[tomul]

You do not need any trig, just basic geometry.
What do you know about the diameter of the circumcircle of a right angled triangle?

The circle is centred on the centre of the hypotenuse and passes through the lower vertex of the triangle where the planes intersect. So doesn't that meant that the height about this point is simply the radius of the circle, half the length of the bar? I've misunderstood something because the height should be a function of $\alpha$.

 

[haruspex]

doesn't that meant that the height about this point is simply the radius of the circle

Not the height above the point, the distance from it.

 

[tomul]

Not the height above the point, the distance from it.

Apologies for the crudely drawn sketch. Is this along the right lines?

$h(\alpha) = \frac{L}{2} sin(\alpha)$

 

[haruspex]

Apologies for the crudely drawn sketch. Is this along the right lines?

$h(\alpha) = \frac{L}{2} sin(\alpha)$

The left hand drawing is ok, but that angle in the right hand drawing is not alpha.
Try drawing some special cases, like alpha=0, alpha=pi/2, or the centre of the rod directly above the intersection.

 

[Delta2]

Interesting problem. Have you tried to solve it using the standard Newtonian method, that is with forces and moments ($\sum F_x=0 ,\sum F_y=0,\sum M=0$ and choosing x and y-axis as the two perpendicular walls. If yes, what do you get?

Even with the Newtonian method you ll have to use some geometry to correctly determine some angles.

 

[Delta2]

Using the Newtonian method (and if I have done the geometry part with angles correct ),I get that $$\frac{1}{\tan a}=\tan 60$$

@haruspex is this correct?

 

[haruspex]

Using the Newtonian method (and if I have done the geometry part with angles correct ),I get that $$\frac{1}{\tan a}=\tan 60$$

@haruspex is this correct?

Yes, the virtual work method gives the same.

 

[ergospherical]

Okay, I've applied the sine rule to find $h(\alpha)$

$\frac{sin\alpha}{h(\alpha)} = \frac{sin(90-\alpha)}{L/2}$
$\frac{sin\alpha}{h(\alpha)} = \frac{2 cos\alpha}{L}$
$h(\alpha) = \frac{L}{2} tan(\alpha)$

Considering a virtual displacement:
$\delta h = h(\alpha + \delta\alpha) = \frac{L}{2} tan(\alpha + \delta\alpha)$
Setting $\delta h = 0$ and therefore $\delta\alpha$=0:
$\frac{L}{2} tan(\alpha) = 0$
$tan(\alpha) = 0$
$\alpha = 0$

which isn't right

I don't think you quite understood. The height of the centre of mass is\begin{align*}
h(\alpha) = \dfrac{L}{2} \left[ \sin{(\alpha)} + \sin{(60 - \alpha)} \right]

\end{align*}Now take the differential,\begin{align*}

\delta h = \dfrac{dh}{d\alpha} \delta \alpha = \dfrac{L}{2} \left[ \cos{(\alpha)} - \cos{(60 - \alpha)}\right] \delta \alpha

\end{align*}If $\delta h = 0$ for some non-zero $\delta \alpha$ then $\cos{(\alpha)} = \cos{(60 - \alpha)}$, thus $\alpha = 30$ corresponds to an equilibrium state.

 

[haruspex]

I don't think you quite understood. The height of the centre of mass is\begin{align*}
h(\alpha) = \dfrac{L}{2} \left[ \sin{(\alpha)} + \sin{(60 - \alpha)} \right]

\end{align*}Now take the differential,\begin{align*}

\delta h = \dfrac{dh}{d\alpha} \delta \alpha = \dfrac{L}{2} \left[ \cos{(\alpha)} - \cos{(60 - \alpha)}\right] \delta \alpha

\end{align*}If $\delta h = 0$ for some non-zero $\delta \alpha$ then $\cos{(\alpha)} = \cos{(60 - \alpha)}$, thus $\alpha = 30$ corresponds to an equilibrium state.

Pursuing a more geometric argument, there is no need for calculus.

 

[ergospherical]

There are a few different ways to find the stationary point of $h(\alpha)$. Aside from differentiation, one may also observe that the trajectory $\boldsymbol{r}(\alpha)$ of the centre of mass is a circle of radius $L/2$ centred on the vertex with the right angle.

 

[tomul]

I don't think you quite understood. The height of the centre of mass is\begin{align*}
h(\alpha) = \dfrac{L}{2} \left[ \sin{(\alpha)} + \sin{(60 - \alpha)} \right]

\end{align*}Now take the differential,\begin{align*}

\delta h = \dfrac{dh}{d\alpha} \delta \alpha = \dfrac{L}{2} \left[ \cos{(\alpha)} - \cos{(60 - \alpha)}\right] \delta \alpha

\end{align*}If $\delta h = 0$ for some non-zero $\delta \alpha$ then $\cos{(\alpha)} = \cos{(60 - \alpha)}$, thus $\alpha = 30$ corresponds to an equilibrium state.

Thank you, I understand your argument now. However, I still can't get the correct expression for $H(\alpha)$. Geometry is a real weak point for me. The problem also states I should use the principle of virtual work, so I don't think that method would be sufficient.

 

[ergospherical]

This method is the principle of virtual work! As per post #2, if the system undergoes a virtual displacement $\delta \alpha$ then the virtual work done is $\delta w^* = -W \dfrac{dh}{d\alpha} \delta \alpha$. The condition for $\delta w^* = 0$ is thus $\dfrac{dh}{d\alpha} = 0$, i.e. equivalent to finding the stationary points of the function $h$.

You could inscribe the triangle in a circle centred on the centre of mass and then observe that the line segment from the vertex with the right angle to the centre of mass divides the triangle into two smaller isosceles triangles.

 

[tomul]

This method is the principle of virtual work! As per post #2, if the system undergoes a virtual displacement $\delta \alpha$ then the virtual work done is $\delta w^* = -W \dfrac{dh}{d\alpha} \delta \alpha$. The condition for $\delta w^* = 0$ is thus $\dfrac{dh}{d\alpha} = 0$, i.e. equivalent to finding the stationary points of the function $h$.

Oh I see. I hadn't seen differentiation used in the context of a virtual work problem before.

You could inscribe the triangle in a circle centred on the centre of mass and then observe that the line segment from the vertex with the right angle to the centre of mass divides the triangle into two smaller isosceles triangles.

This is the approach I've taken as suggested by haruspex but I don't know how to proceed with it. As I say, geometry is a really weak point for me.

 

[haruspex]

This is the approach I've taken as suggested by haruspex but I don't know how to proceed with it. As I say, geometry is a really weak point for me.

Consider a ladder, AB, midpoint M, leaning against a wall. The wall meets the floor at O.
Complete the rectangle AOBC. AB and OC are diagonals of the rectangle crossing at M.
What is the relationship between the lengths AB and OM?
If the ladder slips, what is the path of M?

 

[tomul]

Consider a ladder, AB, midpoint M, leaning against a wall. The wall meets the floor at O.
Complete the rectangle AOBC. AB and OC are diagonals of the rectangle crossing at M.
What is the relationship between the lengths AB and OM?
If the ladder slips, what is the path of M?

AB will be twice OM, and M will move up and to the right

If AB is the radius of the circumcircle of the triangle, $\frac{L}{2}$ then $OM=\frac{L}{4}$. This prompted me to split the height into two sections being sides of two triangles, one with hypotenuse MB and another OM and I've drawn a diagram to show this. This still leaves the task of finding the angles of the triangles to calculate the lengths of the sections, which I attempted to do (in a very long winded way - I think I had the completely wrong approach) but it came out as the wrong answer anyway

 

[haruspex]

M will move up and to the right

Not if the ladder is slipping down.

If AB is the radius of the circumcircle

It is the diameter.

But the important point is that OM is constant. So what is the path of M?