HAgdn
- 23
- 0
- Homework Statement
- Need help if this equation that I thought of would indeed provide right values. I do not have a Tesla meter to compare my values with.
What I am trying to do is solving for the magnetic flux density of produced by a wire with AC voltage. So, I used ohms low (to use voltage as a variable) to calculate for the forwarding and reversing current
Where:
B is Magnetic Flux Density
Micro symbol is permeability
V_peak is the peak voltage of AC current
R is wire resistance (of the wire producing the magnetic field)
r is the distance from the wire producing the field
- Relevant Equations
- B(t)= μ[(V_peak (sinωt ))/R]/2πr
I tried validating the equation by somehow 'solving' only with the involved units.
Magnetic Flux Density – Tesla (T) – Weber (Wb) per square meter (Wb/m2)
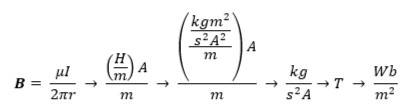
Magnetic Flux Density – Tesla (T) – Weber (Wb) per square meter (Wb/m2)