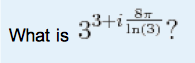Value of an expression involving complex numbers

[Uniman]

View attachment 423

The answer is a number...

Work done so far

3^3 * 3^( i8pi/ln(3) ) = 27 * (3^ i8pi - 3^ln(3) ) = 27 *( 3^25.1i -3.34)

= 3^(3+ i25.1) - 90.26

If this is correct how can I convert this to a number...

 

[chisigma]

Re: Complex function

https://www.physicsforums.com/attachments/423

The answer is a number...

Work done so far

3^3 * 3^( i8pi/ln(3) ) = 27 * (3^ i8pi - 3^ln(3) ) = 27 *( 3^25.1i -3.34)

= 3^(3+ i25.1) - 90.26

If this is correct how can I convert this to a number...

You can use Euler's identity to 'discover' that is...

$\displaystyle 3^{3 + i\ \frac{8\ \pi}{\ln 3}}= e^{3\ \ln 3}= 27$

Kind regards

$\chi$ $\sigma$

 

[soroban]

Re: Complex function

Hello, Uniman!

\text{Evaluate: }\:X \;=\;3^{3 + \frac{8\pi}{\ln(3)}i}

We have: .X \;=\;3^3\cdot3^{\frac{8\pi}{\ln(3)}i} \;=\;27\cdot 3^{\frac{8\pi}{\ln(3)}i} .[1]

\text{Let }y \:=\:3^{\frac{8\pi}{\ln(3)}i}

\text{Take logs: }\:\ln(y) \;=\;\ln\left(3^{\frac{8\pi}{\ln(3)}i}\right) \;=\;\frac{8\pi}{\ln(3)}i\cdot\ln(3) \;=\;8\pi i

. . y \;=\;e^{8\pi i} \;=\;\left(e^{i\pi}\right)^8 \;=\;(\text{-}1)^8 \;=\;1Substitute into [1]: .X \;=\;27\cdot1 \;=\;\boxed{27}