Variation of the lightning train thought experiment

[FeynmanFtw]

TL;DR Summary

Getting to grips with a variation of Einstein's train lightning thought experiment

Hi all,

I've been going over some special relativity as it's a topic I never really studied during my younger years and wanted to get to grips with it, especially since it's such a fundamental part of our understanding of the cosmos.

I was reading about Einsteins train lightning thought experiment the other day, and although that example makes sense, I created my own thought experiment that seems to have caused a bit of a discussion between myself and a colleague.

Imagine we have an observer (P) standing on the platform, midway along the platform. Say the platform is 1 km long (for the sake of brevity). They observe two lightning strikes either end of the platform (A and B) occur simultaneously in their reference frame. However, we have another observer on the train (P'), travelling at some velocity v, passing the platform on one end (A) exactly as the lightning strikes, instead of being midway along the platform as in the original thought experiment.

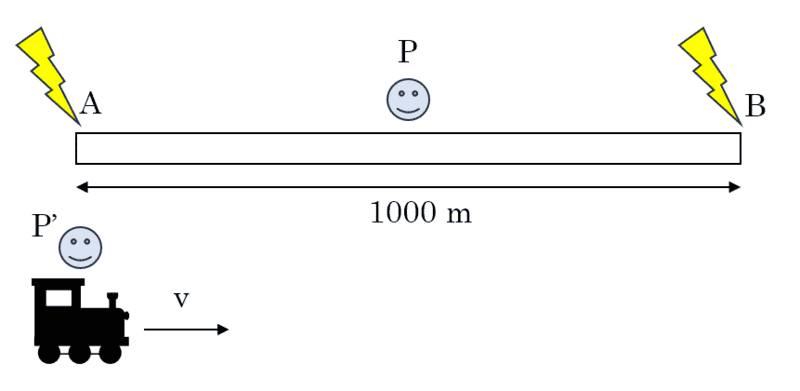
Now we can imagine that at low speeds (v << c), P' would observe A occur before B, because the light from B would have to take some time to travel to reach the train from the other side of the platform, which would have hardly moved at all relative to the speed of light.

However, take the case that the train is now moving at a significant fraction of the speed of light, say 0.6c (so gamma is 1.25). My colleague states that the train should observe B occur before A, given the calculation:

$$t' = \gamma(t - \frac {vx} {c^2}) = 1.25(0 - \frac {(0.6c)(1000)} {c^2}) = -2.5 \mu s$$

He says that you can imagine, relative to the train, the platform is moving at 0.6c towards them, hence why lightning B will be seen first. But I think this is wrong. The train moves past the platform at exactly the point when lightning A strikes the platform, and given that the distance between train and platform can be taken to be negligible (this is the first variant, I discuss where this distance is relevant further below), the train should observe this flash the instant it occurs. Light will be travelling at c and therefore overtake the train the instant the lightning strikes, meaning that the train should still observe A before B. But I'm not sure how to prove this, I must admit.

This is the first conundrum.

The second is that, we think the situation must definitely depend on the position of the train relative to the platform. Take these 3 scenarios:

Scenario 1 - Train is midway along the platform (akin to Einsteins thought experiment). We know that P' will observe B before A.
Scenario 2 - Train is approaching the platform, from the side of A. It must observe A first and then B, simply because A is closer.
Scenario 3 - Train is far away from the platform. Along the axis of the platform, what must be the distance of the train in order to see lightning A occur first, A and B to occur together and B to occur before A?

Any help answering these questions would be very helpful.

 

[PeroK]

First, Einstein's lightning thought experiment is overcomplicated and confusing. I always suggest ignoring it, as there are many simpler and better ways to demonstrate the relativity of simultaneity.

That said, I do confess that no student has ever heeded my advice!

Second, SR does not depend on the finite travel time of a light signal from an event to an observer. The delay in a signal reaching an observer has always been taken into account and factored out of any calculations. In fact, this is how the speed of light was first estimated several hundred years ago.

In particular, the measured time of an event cannot depend in the position of an observer.

I suspect your arguments, therefore, are based on this misconception.

 

[Hill]

If the strikes A and B are simultaneous in the P reference frame, then the strike B occurs before the strike A in the P' reference frame. This relates the times when the strikes occur and not the time when they are observed.

 

[PeroK]

For a simpler treatment of the basics of SR try chapter 1 of Morin's book, which is available free here:
https://scholar.harvard.edu/david-morin/special-relativity

 

[FeynmanFtw]

First, Einstein's lightning thought experiment is overcomplicated and confusing. I always suggest ignoring it, as there are many simpler and better ways to demonstrate the relativity of simultaneity.

That said, I do confess that no student has ever heeded my advice!

Second, SR does not depend on the finite travel time of a light signal from an event to an observer. The delay in a signal reaching an observer has always been taken into account and factored out of any calculations. In fact, this is how the speed of light was first estimated several hundred years ago.

In particular, the measured time of an event cannot depend in the position of an observer.

I suspect your arguments, therefore, are based on this misconception.

Forgive my ignorance but I cannot see how this explicitly disproves my assertion. Can you explain your point a bit further?

 

[vanhees71]

The light signal from A will be simultaneously seen by both observers at $t=t'=0$.

The light signal from A in P's frame moving to the right is described by the world line
$$x_A=(c t,ct).$$
It reaches the observer when $x_A^1=L/2$, i.e., at time $t_A=L/(2c)$, where $L$ is the length of the platform.

The light signal from B in P's frame moving to the left is described by the world line
$$x_B=(c t,L-c t),$$
Obviously it reaches the observer when $x_B^1=L/2$, i.e., at the time $t=L/(2c)$.

In the same frame the world line of P' is described by
$$x_{P'}=(c t,v t).$$
He sees the light signal $A$ if $x_A^1-x_{P'}^1=(c-v)t=0$ since $v<c$ this is at $t=0$.
For signal B
$$x_B^1-x_{P'}^1=L-(c+v) t=0 \; \Rightarrow t=\frac{L}{c+v}>L/(2c),$$
i.e., the light signal reaches observer $P'$ still later than observer $P$.

I don't see, where there is anything specifically relativistic here.

 

[PeroK]

Forgive my ignorance but I cannot see how this explicitly disproves my assertion. Can you explain your point a bit further?

I wasn't trying to disprove your assertion. I was simply indicating that you have misunderstood the basics.

 

[Dragon27]

Forgive my ignorance but I cannot see how this explicitly disproves my assertion. Can you explain your point a bit further?

When you say "P' observes" you mean "light from the event reaches P'", when your colleague says "P' observes" he means (whether he realizes it or not) "event happens in the frame of reference of P'". In other words, P' sees the light from the event and then calculates backwards when the event should have happened, given the light should have taken some time to reach them.

 

[FeynmanFtw]

I wasn't trying to disprove your assertion. I was simply indicating that you have misunderstood the basics.

That's not really helpful, but I appreciate the input nonetheless.

When you say "P' observes" you mean "light from the event reaches P'", when your colleague says "P' observes" he means (whether he realizes it or not) "event happens in the frame of reference of P'". In other words, P' sees the light from the event and then calculates backwards when the event should have happened, given the light should have taken some time to reach them.

Ok, I think this is starting to make sense. So according to P', they will actually see the light from B after A, but will deduce that B occurred before A?

 

[Dale]

My colleague states that the train should observe B occur before A, given the calculation

Your disagreement with your colleague may stem from the use of the word “observe”. Unfortunately it is often used in two confusingly different ways.

“Observe” may mean what one directly sees. The raw sensory experience or measurement. E.g. on my 50th birthday I observed a star go nova.

“Observe” may also mean what one infers from the raw sensory experience or measurement after accounting for the finite speed of light. E.g. I observed that a star 50 light years away went nova on the day that I was born.

I believe you are using it in the first sense and your friend is using it in the second sense. If so you are both correct. You are talking about the order of receiving the light by the train (left flash first, right flash second). Your colleague is talking about the order of the emission of the light in the train’s frame (right flash first, left flash second)

 

[Ibix]

Ok, I think this is starting to make sense. So according to P', they will actually see the light from B after A, but will deduce that B occurred before A?

Yes. The usual train thought experiment is set up so that each observer is equidistant from the emissions, so if they see the flashes simultaneously they deduce that they were emitted simultaneously. You then show that both observers cannot see the flashes simultaneously so they must have different deductions about the simultaneity.

Unfortunately a lot of sources (me included, from time to time) are sloppy and use the word "see" to refer to deductions about events rather than direct observations. Coupled with this particular thought experiment where you don't need to explicitly do the maths and subtract out the light travel time to get the point, and it's not surprising that people get the wrong end of the stick.

 

[PeroK]

... it seems to me that in this instance, great man though he was, Einstein is poking the student in the eye with the wrong end of the stick!

 

[Dragon27]

Ok, I think this is starting to make sense. So according to P', they will actually see the light from B after A, but will deduce that B occurred before A?

Yep. And of course the light from B will hit them after the light from A. That what happens from the point of view of the observer P (the one in the middle of the platform), and this sequence of events (i.e. the order of lights flashing on P') should not depend on the observer.

 

[FeynmanFtw]

Yes. The usual train thought experiment is set up so that each observer is equidistant from the emissions, so if they see the flashes simultaneously they deduce that they were emitted simultaneously. You then show that both observers cannot see the flashes simultaneously so they must have different deductions about the simultaneity.

Unfortunately a lot of sources (me included, from time to time) are sloppy and use the word "see" to refer to deductions about events rather than direct observations. Coupled with this particular thought experiment where you don't need to explicitly do the maths and subtract out the light travel time to get the point, and it's not surprising that people get the wrong end of the stick.

Thank you, this makes things a lot clearer, and I will admit that this ties in with the concept that I'm struggling with intuitively.

See, my mistake (as it's apparently so) comes from assuming the observations (as in detections) are relative, but the events themselves are not. I cannot imagine how P' can deduce B happened before A (signifying an 'absolute' sense of occurance) when in the frame of the platform they occurred simultaneously...I suspect I've probably got the wrong idea that many have while trying to overcome the confusion inherent in SR.

 

[PeroK]

Thank you, this makes things a lot clearer, and I will admit that this ties in with the concept that I'm struggling with intuitively.

See, my mistake (as it's apparently so) comes from assuming the observations (as in detections) are relative, but the events themselves are not. I cannot imagine how P' can deduce B happened before A (signifying an 'absolute' sense of occurance) when in the frame of the platform they occurred simultaneously...I suspect I've probably got the wrong idea that many have while trying to overcome the confusion inherent in SR.

The first postulate of SR is that the speed of light is invariant across all inertial reference frames. That is incompatible with intuitive ideas of space, time and simultaneity. Once you have committed to the first postulate, you need some imagination to follow the logical consequences.

 

[Dale]

... it seems to me that in this instance, great man though he was, Einstein is poking the student in the eye with the wrong end of the stick!

Is there a right end of the stick to poke a student in the eye with?

 

[Dale]

this sequence of events (i.e. the order of lights flashing on P') should not depend on the observer.

But it does.

Suppose that you have two events and in some given inertial frame the distance between them is $dx$ and in that same inertial frame the time between them is $dt$. It turns out that the quantity $ds^2 = -c^2 dt^2 + dx^2 + dy^2 + ds^2$ is something that all frames agree on. It is an invariant quantity called the spacetime interval.

When $ds^2<0$ then the interval is called timelike and all reference frames agree on the order. But when $ds^2>0$ the interval is called spacelike and in some reference frames the order of the two events will be reversed. When $ds^2=0$ the interval is called lightlike or null, and it represents a flash of light (the order of emission and reception is agreed by all frames since emissions cause receptions).

This is important because if one event causes another then since causes must come before effects that means that all frames must agree on the order of the cause and the effect. So events that are spacelike separated cannot have a cause-effect relationship. Only for such events can the order change. Nature "cares" about the order of causes and effects, but the order of other events is just a matter of human convention.

One other very useful thing about the spacetime interval is that when the interval is timelike ($ds^2<0$) then $d\tau=\sqrt{-ds^2/c^2}$ is called the proper time and represents the time on a clock that went straight from one event to the other.

 

[Dragon27]

But it does.

When $ds^2<0$ then the interval is called timelike and all reference frames agree on the order.

Yes, that is exactly what I meant, I just didn't want to mention terms like "time-like interval" and "causally connected". The light flashes on the moving train (where P' is located) are separated by a time-like interval (as are any events that happen on a real moving body, that we can consider point-like). Maybe the way I said it could have caused confusion, by I meant the events of the light (that originated on one of the end of the platform) reaching the eyes of the observer on the moving train.
The two flashes of the light on the ends of the platform, on the other hand, i.e. the events that happen at the ends of the platform at the same time from the point of the view of the observer standing in the middle of the platform (i.e. P) are space-like separated, so their order is fair game.

 

[Mister T]

I cannot imagine how P' can deduce B happened before A (signifying an 'absolute' sense of occurance) when in the frame of the platform they occurred simultaneously...

Because the speed of light is the same for both observers. That's the whole point of the thought experiment.

 

[FactChecker]

However, we have another observer on the train (P'), travelling at some velocity v, passing the platform on one end (A) exactly as the lightning strikes, instead of being midway along the platform as in the original thought experiment.

View attachment 338302

Now we can imagine that at low speeds (v << c), P' would observe A occur before B, because the light from B would have to take some time to travel to reach the train from the other side of the platform, which would have hardly moved at all relative to the speed of light.

This is a common mistake that unnecessarily complicates things. An Inertial Reference Frame has its own time and space coordinates everywhere. You should think of an "observer" as representing how an inertial reference frame would record events in its spacetime coordinate system, regardless of where the event happens. An "observer" records the IRF's time immediately at the location of every event, even if events are separated by great distances. Those times are used in calculations.
The time dilation of Special Relativity is never enough to switch the order of two events that have a cause/effect relationship.

 

[Sagittarius A-Star]

I was reading about Einsteins train lightning thought experiment the other day, and although that example makes sense, I created my own thought experiment that seems to have caused a bit of a discussion between myself and a colleague.

I doubt, that you understood the intention of Einstein's thought experiment, as described by @Dragon27 .
You should read his thought experiment carefully. For didactic reasons it makes sense to have a very long train.

It is essential in his thought experiment, that ...

• ... the embankment observer stays permanently in the middle $M$ between the embankment-locations of both lightning strikes and that he defines, that both light pulses need the same coordinate-time to reach him over the same coordinate-distances (with reference to the embankment-rest frame).
• ... the train observer stays permanently in the middle $M'$ between the train-locations of both lightning strikes and that he defines, that both light pulses need the same coordinate-time to reach him over the same coordinate-distances (with reference to the train-rest frame).

 

[vanhees71]

The first postulate of SR is that the speed of light is invariant across all inertial reference frames. That is incompatible with intuitive ideas of space, time and simultaneity. Once you have committed to the first postulate, you need some imagination to follow the logical consequences.

To put it more simply: Einstein's 2nd postulat says that the speed of light in vacuum is independent on the motion of both the light source wrt. to the restframe of the detector.