Vec norm in polar coordinates differs from norm in Cartesian coordinates

[cianfa72]

Just as an example consider the following picture:

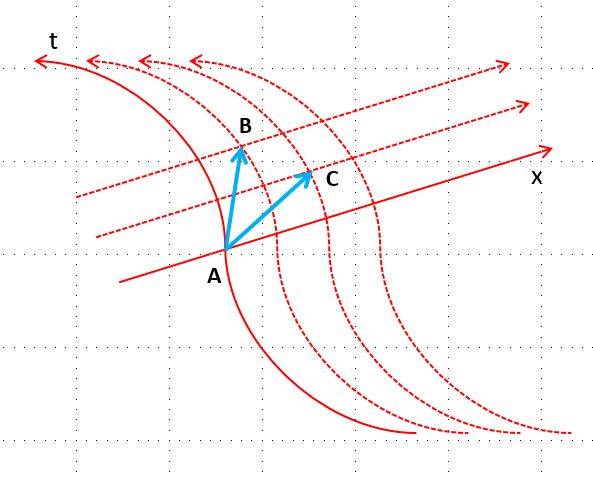
It is the affine 2-plane in a curvilinear coordinate system. The position vector field is still defined at each point as long as an origin A is chosen (since it depends on the definition of affine space alone). The components of the position vector field evaluated at point B or C depend on the coordinate/holonomic basis vectors associated to the curvilinear coordinate system at point B or C respectively.

 

[Dale]

An affine space - which was the context of the quoted text - is flat.

Agreed. But the OP asks first about manifolds, and then specializes the question to a flat manifold. So keeping the distinctions doesn’t hurt and could alleviate some confusion for people who may not be familiar with the portions of the conversation that are valid for all manifolds and the portions that only apply for flat manifolds.

 

[Orodruin]

Agreed. But the OP asks first about manifolds, and then specializes the question to a flat manifold. So keeping the distinctions doesn’t hurt and could alleviate some confusion for people who may not be familiar with the portions of the conversation that are valid for all manifolds and the portions that only apply for flat manifolds.

Sure, just saying that the statement was clearly about affine spaces so saying that you disagree with it is a bit confusing as well. I assume you do not disagree with the statement for affine spaces.

 

[Dale]

Sure, just saying that the statement was clearly about affine spaces so saying that you disagree with it is a bit confusing as well. I assume you do not disagree with the statement for affine spaces.

Sorry, I should have been clear what I was disagreeing with. I disagree that there is no need to make the distinction. The statement was valid, but without the distinction it could be confusing. So I think there is a need to make the distinction. And it doesn’t hurt your argument to do so.

 

[vanhees71]

Can "flat" even be defined for an affine space?

The affine space uses the obvious connection, making it flat automatically.

 

[cianfa72]

Suppose to slightly bend a plane without changing its topology. Do you think the resulting manifold retains the structure of affine space ?

 

[Dale]

The affine space uses the obvious connection, making it flat automatically.

And parallel transport is not path dependent with the obvious connection. Which, as you say, makes it flat.

 

[Dale]

Suppose to slightly bend a plane without changing its topology. Do you think the resulting manifold retains the structure of affine space ?

That is too vague. You can bend a plane and introduce extrinsic curvature but not intrinsic curvature or you can bend it to introduce intrinsic curvature.

 

[cianfa72]

You can bend a plane and introduce extrinsic curvature but not intrinsic curvature or you can bend it to introduce intrinsic curvature.

Latter case without altering the topology of the plane.

 

[DrGreg]

Latter case without altering the topology of the plane.

"Topology" is the wrong word to use here. It's the (2D) metric that doesn't alter, which is a stronger condition.

 

[Orodruin]

I disagree that there is no need to make the distinction.

The entire point of my post was that there is no need to make a distinction in an affine space, which was the context of the post. I do not see how you can disagree with this.

In a general manifold there is no translation vector space to identify with the tangent space so the statement clearly does not apply there.

 

[cianfa72]

"Topology" is the wrong word to use here. It's the (2D) metric that doesn't alter, which is a stronger condition.

The idea is to introduce intrinsic curvature (hence the 2D metric changes) without changing the topology (the bent plane with its curved intrinsic geometry is still globally homeomorphic to the plane with standard topology).

My question is: can we still define an affine structure for it ? In other words, starting from the set of points, can we define a translation vector space such that the axioms of affine space are met ?

 

[Orodruin]

The idea is to introduce intrinsic curvature (hence the 2D metric changes) without changing the topology (the bent plane with its curved intrinsic geometry is still globally homeomorphic to the plane with standard topology).

My question is: can we still define an affine structure for it ? In other words, starting from the set of points, can we define a translation vector space such that the axioms of affine space are met ?

No. Any affine space is flat and a (intrinsically) curved space is not flat by definition.