Vector addition and subtraction

[Slimy0233]

Homework Statement

Use the cross product to find the components of the unit vector ˆn perpendicular to the shaded
plane in Fig. 1.11.

Relevant Equations

O1 = O2 + O12

Mentor note: Moved from General Math section, so is missing the homework template.

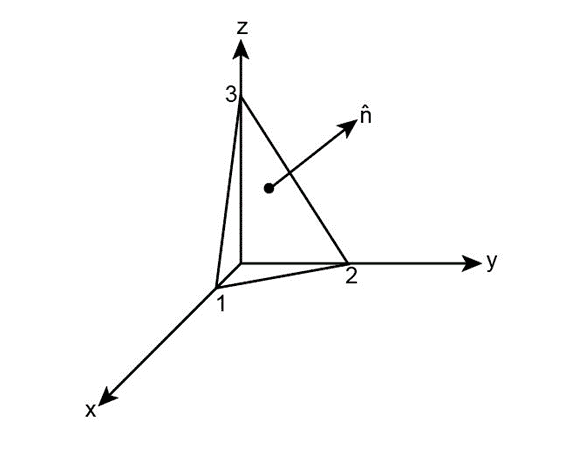
If you want the vector which represents the base from 1 to 2 (or O1 to O2 are the position vectors, I am using co-ordinates as names), what would O12 (vector from 1 to 2) and why?
1. Would it be O1 - O2 or O1 + O2? and why?

I got the wrong answer when I assumed O1 + O2, but I don't understand why? What's the difference?

 

[Mark44]

Mentor note: Moved from General Math section, so is missing the homework template.View attachment 327562
If you want the vector which represents the base from 1 to 2 (or O1 to O2 are the position vectors, I am using co-ordinates as names), what would O12 (vector from 1 to 2) and why?
1. Would it be O1 - O2 or O1 + O2? and why?

I got the wrong answer when I assumed O1 + O2, but I don't understand why? What's the difference?

For clarity I'm going to rename points 1 and 2 as points A and B, respectively, and O is the origin. By vector addition, OA + AB = OB, so AB = OB - OA.

 

[Slimy0233]

For clarity I'm going to rename points 1 and 2 as points A and B, respectively, and O is the origin. By vector addition, OA + AB = OB, so AB = OB - OA.

I understand what you are trying to say completely, but in purely a mathematical way, I can't add O1 and O2 because, it doesn't make much sense as in order to add two vectors the head of the first vector should be at the tail of the second vector or vice versa, am I right?
So, when I add vec(O1) and vec(O2), I am not getting vec(12), but rather I am getting a vector which would point to i + 2 j, which basically is like the middle point of those vectors (not really, but I lack the vocabulary to explain it). It makes sense now.also, I feel like I can also imagine this in a different way, a person can't travel in two directions simultaneously, so it doesn't make sense to add O1 and O2? Are my ways of interpreting this acceptable?

PS: Hey mentor, did you move this from vectors forum to help forum. It's not actually HW though, so I am not sure what the procedure was. It's a question from Griffiths which you can see here[the answer is wrong] Should I still have posted this on HW help even if it's not really HW (I am sorry, I haven't read all the rules yet, just the main ones]

 

[Mark44]

I understand what you are trying to say completely, but in purely a mathematical way, I can't add O1 and O2 because, it doesn't make much sense as in order to add two vectors the head of the first vector should be at the tail of the second vector or vice versa, am I right?

No, not right. You can move vectors around as long as the move is strictly a translation that preserves the direction and length of the vector.

So, when I add vec(O1) and vec(O2), I am not getting vec(12), but rather I am getting a vector which would point to i + 2 j, which basically is like the middle point of those vectors (not really, but I lack the vocabulary to explain it).

Yes. At first I didn't pick up on vector O1 having its head at the point (1, 0) and similarly for vector O2. You can write these two vectors as <1, 0> and <0, 2>. Adding them would result in the vector <1, 2> or as you wrote it, i + 2j.

PS: Hey mentor, did you move this from vectors forum to help forum. It's not actually HW though, so I am not sure what the procedure was. It's a question from Griffiths which you can see here[the answer is wrong] Should I still have posted this on HW help even if it's not really HW (I am sorry, I haven't read all the rules yet, just the main ones]

Yes I moved it, based on a report from another mentor. It's enough like a homework question that the current section is where it belongs.

BTW, which part of the answer in Griffith do you believe is wrong? At a quick scan of the page, the work there looks fine to me.

 

[berkeman]

PS: Hey mentor, did you move this from vectors forum to help forum. It's not actually HW though, so I am not sure what the procedure was. It's a question from Griffiths which you can see here[the answer is wrong] Should I still have posted this on HW help even if it's not really HW (I am sorry, I haven't read all the rules yet, just the main ones]

Per the PF rules, all schoolwork-type questions should go in the Homework Help forums, and not in the technical forums. The quote below is from the Rules (see INFO at the top of the page):

Posts Belong in the Homework Forum
Any and all high school and undergraduate homework assignments or textbook-style exercises for which you are seeking assistance are to be posted in the appropriate forum in our Homework & Coursework Questions area--not in blogs, visitor messages, PMs, or the main technical forums. This should be done whether the problem is part of one's assigned coursework or just independent study. The reason for this is that the scientific and mathematical sections of Physics Forums are to be reserved for discussions and not academic assistance.

 

[Slimy0233]

No, not right. You can move vectors around as long as the move is strictly a translation that preserves the direction and length of the vector.

@Mark44 Thank you very much for that. But I kinda have a doubt regarding this. Even when you move vectors around, aren't you really bringing the vectors such that one vector's tail is at another's head?

If I am not articulate enough, this might aid what I am trying to say


> BTW, which part of the answer in Griffith do you believe is wrong? At a quick scan of the page, the work there looks fine to me.

actually, they are slightly wrong, but I am pretty sure it's a calculation mistake. No solution is given in the book, it's just one of the exercises.

The answer should be 1/7*(6,3,2) as I have shown above, ignore the first page.

 

[Slimy0233]

Per the PF rules, all schoolwork-type questions should go in the Homework Help forums, and not in the technical forums. The quote below is from the Rules (see INFO at the top of the page):

hey, I am sorry for this. I must have read the rules thoroughly, which I will do soon enough. But while it comes to the rule you have kindly included in your reply, these type of questions are thought of as HW type questions and I can see why. But if you have theoretical questions, you can post this in the main forums right? I mean, theoretical doubts essentially like "What would be the intensity of light that would be observed during metal welding and why?" or something about vectors I dont' understand in Griffiths but is not like a question as it is here . I did read the rule, but I just had this doubt.

 

[berkeman]

But if you have theoretical questions, you can post this in the main forums right? I mean, theoretical doubts essentially like "What would be the intensity of light that would be observed during metal welding and why?"

Usually that should qualify for the technical forums, but you can always PM a Mentor to check to be sure. It's sometimes a judgement call on whether the question could be for a points-paying schoolwork assignment. This old thread will help to explain the PF approach to schoolwork-type questions:

https://www.physicsforums.com/threads/homework-coursework-questions.373889/

 

[Slimy0233]

Usually that should qualify for the technical forums, but you can always PM a Mentor to check to be sure.

tbh, I hate to annoy mentors with trivial questions, (Ik you have got stuff to do). I mean, I would say in an ideal forum, there should not be much jobs for the moderator.

somewhat ironic that I am saying this but ok. I will read the rules throughly by tmr. Thank you for what you do here.

 

[Mark44]

Even when you move vectors around, aren't you really bringing the vectors such that one vector's tail is at another's head?

That's not really different from what I said. As long as you move them rigidly, it doesn't matter.

actually, they are slightly wrong,

The answer should be 1/7*(6,3,2) as I have shown above, ignore the first page.

You're right, because their final vector isn't a unit vector. The vector <6, 3, 2> has a magnitude of $\sqrt{49}$. I've gone through their work in detail, and can't find where they went wrong.

 

[Mark44]

actually, they are slightly wrong, but I am pretty sure it's a calculation mistake.

It's worse than "slightly wrong" -- they have made a pretty serious mistake, one that I'm surprised to see in a book as well-known as Griffith's.
What they did was to calculate unit vectors $\hat{r_1}$ and $\hat{r_2}$, and then crossed them to get $\frac 1 {\sqrt{50}}< 6, 3, 2>$. Their mistake is in thinking that the cross product of unit vectors is also a unit vector. This happens if and only if the vectors being crossed happen to be perpendicular to each other. For the problem in this thread, the vectors are not perpendicular (their dot product is nonzero), so the result of crossing the unit vectors above has the right direction but isn't a unit vector.

 

[DrClaude]

It's worse than "slightly wrong" -- they have made a pretty serious mistake, one that I'm surprised to see in a book as well-known as Griffith's.

That answer is not from Griffiths. I have checked the solution manual and Griffiths explicitly says that the result of the cross product has to be normalized, and the answer he gives is the correct one.

 

[Slimy0233]

That's not really different from what I said. As long as you move them rigidly, it doesn't matter.
You're right, because their final vector isn't a unit vector. The vector <6, 3, 2> has a magnitude of $\sqrt{49}$. I've gone through their work in detail, and can't find where they went wrong.

Yesterday at 10 PM: I will do that first thing in the morning. I should be learning from others mistake too ig.

Today: Even though I planned on solving it, didn't get enough time. I am glad you highlighted the mistake tho! @Mark44

Also I am sorry, I think I told you that it's not the solution given by Griffiths himself, but it's an exercise which the readers are supposed to solve as @DrClaude pointed out.

I really thought I mentioned it in my reply but I see that I didn't do so. My fault

 

[Mark44]

Also I am sorry, I think I told you that it's not the solution given by Griffiths himself, but it's an exercise which the readers are supposed to solve

In the PDF at the top it says "Griffiths Electrodynamics 4e: Problem 1.4" -- I assumed this work came from the textbook itself. I don't have this textbook, so couldn't verify this for myself.