Vector addition, trying to find the angle

[Ineedhelpwithphysics]

Homework Statement

IN picture

Relevant Equations

Addition of angles

Is angle Vag 180 since the vector is a straight line pointing left?
Also you can add 30 degrees with 150 which will be 180?

 

[kuruman]

Yes, the wind velocity vector forms an angle of 180° with the positive x-axis.
Adding 30 degrees to 150 degrees will always give you 180 degrees, but that is not the angle that the resultant you are looking for forms relative to the positive x-axis.

By the way, "Addition of angles" is not an equation.

 

[vela]

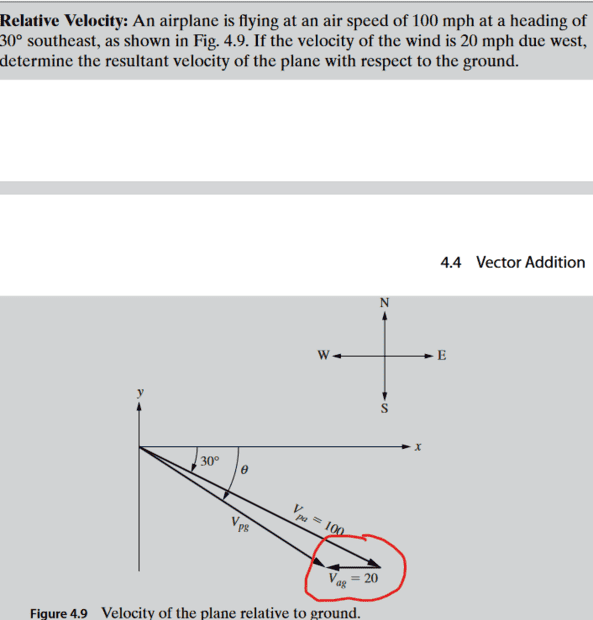
Also you can add 30 degrees with 150 which will be 180?

How is this relevant to solving the problem? Just because you can combine two numbers given in the problem to produce a third doesn't mean you should do it. You need to have a valid reason for doing so.

When it comes to vector addition, you have three basic building blocks. First, you can resolve a vector into components. If a vector $\vec A$ has magnitude $A$ and direction $\theta$ (relative to the +x axis), its components are $A_x = A \cos\theta$ and $A_y = A \sin\theta$. Second, you can go the other way: if you know the components of a vector, its magnitude is $A = \sqrt{A_x^2 + A_y^2}$ and its direction satisfies $\tan \theta = A_y/A_x$. Finally, you have the rule about how to actually add the vectors: if $\vec C = \vec A + \vec B$, then $C_x = A_x + B_x$ and $C_y = A_y + B_y$.

Using just those building blocks, can you come up with a way to use them to solve the problem at hand?