- #1
Electro
- 48
- 0
Hello Everyone,
In school I had a test of Vector exercises. The problem is that I have to submit them online and I need the exact value for the questions. Anyway I don't want you to solve them for me. I just need some help where I am stuck.
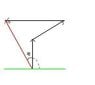
The first exercise: A boy runs 3.3 m North, 7.1 m NorthEast and 15.6 m West. a)Determine the length of the displacement vector tha goes from the starting point to his final position. b)Determine the direction of the displacement vector.
I was confused by this exercise because there isn't any angle given. So I assumed that "NorthEast" means that he moves 7.1 m with an angle 45 Deg.
Then part a) is easy. For part b) I found the angle formed by the North line and the Resultant vector. Am I right here?
The next exercise is a little fuzzy I think: Let aA + bB + C=0, where
A=(17,-99), B=(-99,28) and C=(4.3,78), where Ax=17 units, Ay=-99 units etc. What is the value of a and b? (All the Upper case letters A,B and C have the vector arrow above).
What I did is: I opened aA + bB + C=0 using unit vectors i, j and k (k=0) and the numbers given above.
Still I have a and b and it's an equation with 2 unknowns.
The final expression I concluded is: (a*17i-b*99i+4.3i)+(b*28j-a*99j+78j)=0...?
What I think now, is forming two simultaneous equations.
1) 17a-99b= -4.3
2) 28b-99a= -78
Solving them, I think is the answer for a and b.
Since the i units can't be added to the j units I formed two equations just neglecting i and j (the brackets give 0). So for i group it will give 0 and for j group too.
Please I need an answer whether I am right or not.
Thank you
Electro
In school I had a test of Vector exercises. The problem is that I have to submit them online and I need the exact value for the questions. Anyway I don't want you to solve them for me. I just need some help where I am stuck.
The first exercise: A boy runs 3.3 m North, 7.1 m NorthEast and 15.6 m West. a)Determine the length of the displacement vector tha goes from the starting point to his final position. b)Determine the direction of the displacement vector.
I was confused by this exercise because there isn't any angle given. So I assumed that "NorthEast" means that he moves 7.1 m with an angle 45 Deg.
Then part a) is easy. For part b) I found the angle formed by the North line and the Resultant vector. Am I right here?
The next exercise is a little fuzzy I think: Let aA + bB + C=0, where
A=(17,-99), B=(-99,28) and C=(4.3,78), where Ax=17 units, Ay=-99 units etc. What is the value of a and b? (All the Upper case letters A,B and C have the vector arrow above).
What I did is: I opened aA + bB + C=0 using unit vectors i, j and k (k=0) and the numbers given above.
Still I have a and b and it's an equation with 2 unknowns.
The final expression I concluded is: (a*17i-b*99i+4.3i)+(b*28j-a*99j+78j)=0...?
What I think now, is forming two simultaneous equations.
1) 17a-99b= -4.3
2) 28b-99a= -78
Solving them, I think is the answer for a and b.
Since the i units can't be added to the j units I formed two equations just neglecting i and j (the brackets give 0). So for i group it will give 0 and for j group too.
Please I need an answer whether I am right or not.
Thank you
Electro