Vector field and differential form confusion

[Lips]

Homework Statement

We have xy-plane, which is has a mapping (x,y). Another map is (u,v) and the transformation of coordinates are u=4x+3y and v=x+y.

1. Write vector field \frac{\partial}{\partial u} in the map (x,y)

2. Write the 1-form du in the map (x,y)

Relevant Equations

u=4x+3y and v=x+y.

Here is a picture of the solution I made :

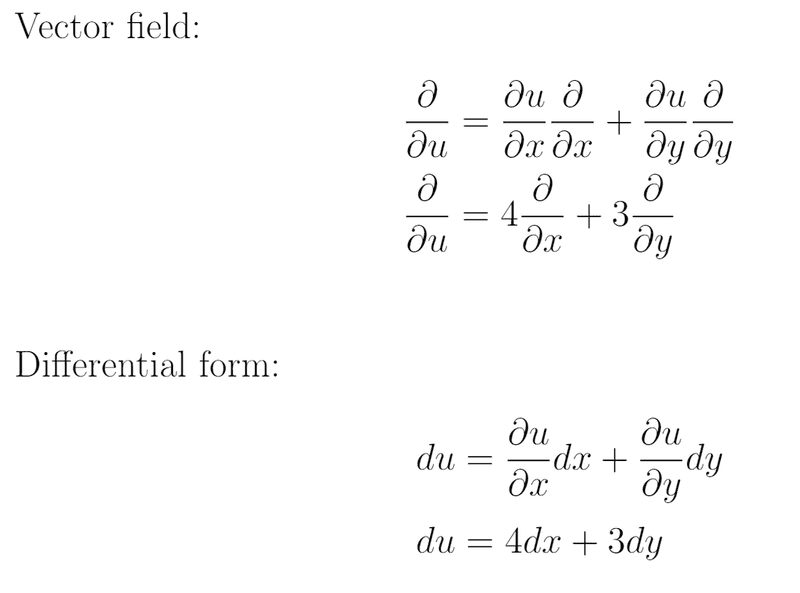So my question is: Are these right and how do they differ from each other?

 

[WWGD]

In a formal Mathematical sense, they're duals to each other. Differential forms are evaluated at Vector Fields to produce numbers.

 

[Gavran]

$\text { The first thing: }$
$\frac { \partial } { \partial u } \text { is not a vector field. }$

$\text { The second thing: }$
$\text { The expression } \frac { \partial } { \partial u } = \frac { \partial u } { \partial x } \frac { \partial } { \partial x } + \frac { \partial u } { \partial y } \frac { \partial } { \partial y } \text { is not a correct expression. }$
$\text { It should be } \frac { \partial } { \partial u } = \frac { \partial x } { \partial u } \frac { \partial } { \partial x } + \frac { \partial y } { \partial u } \frac { \partial } { \partial y } \text { where } x \text { and } y \text { are functions of } u \text { and } v \text { . }$