- #1
Lajka
- 68
- 0
Hi
I thought about putting this topic in physics subforum, but I think it's overall more fitting here.
So, I'm having problems understanding some basic stuff, and I'm kinda embarassed. I'm an engineer and I'm trying to sort things I already know but on a more rigorous mathematic foundation, and then I get confused from time to time, such as now.
Anyway, let's say we have a parametric vector-valued function [tex]r(t)=(x(t),y(t))[/tex]
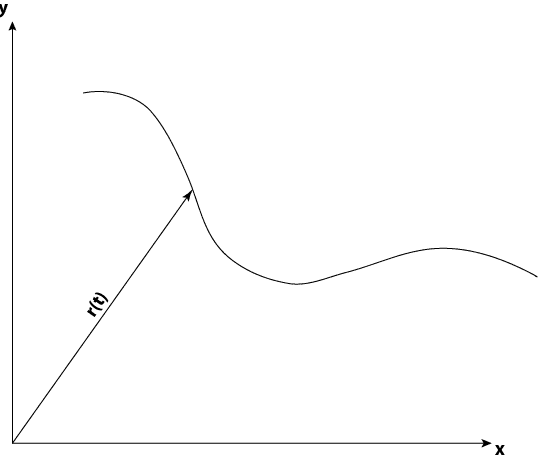
Nothing too fancy, just your everyday normal trajectory. Now, if we define a derivative of this function as
[tex]\dot{r}(t)=\frac{dr(t)}{dt}=(\dot{x}(t),\dot{y}(t))[/tex]
it is said that this represents the velocity of a function in all the points of the curvature [tex]r(t)[/tex].
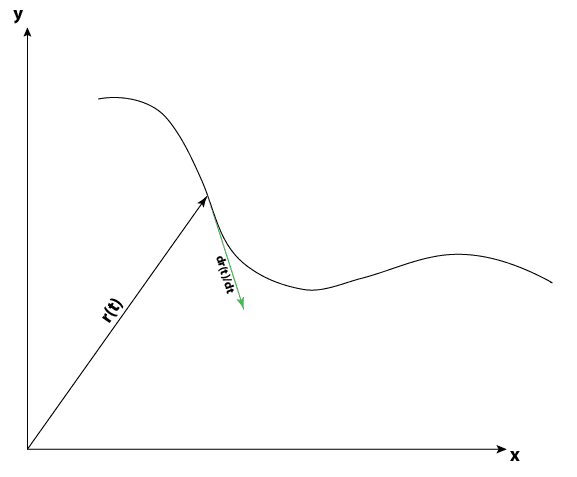
Therefore, it must be a vector field, by its nature. And now that I think about it, I can't seem to understand this. For something to be a vector field, it must have an input vector and an output vector. For me, [tex]\dot{r}(t)[/tex] is just another parametric vector-valued function, with a scalar as an input, that's all I see.
Moreover, let's recall the definition of a derivative
[tex]\dot{r}(t)=\frac{dr(t)}{dt}=lim_{\Delta t \rightarrow 0} \frac{r(t + \Delta t) - r(t)}{\Delta t}[/tex]
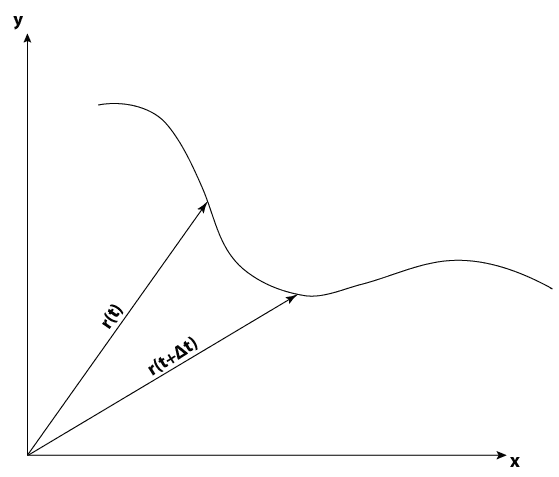
But what exactly is [tex]{r(t + \Delta t) - r(t)[/tex]? Is it this?
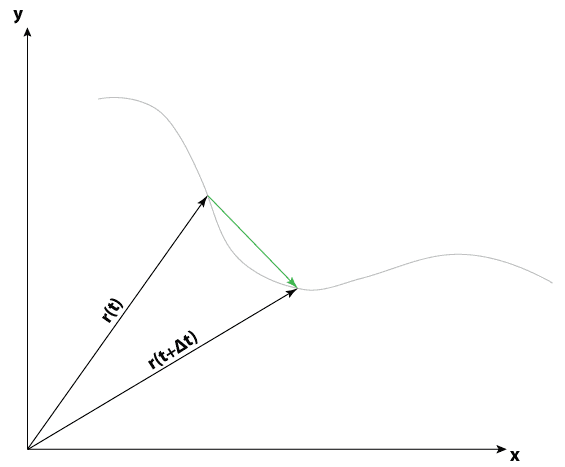
or this?
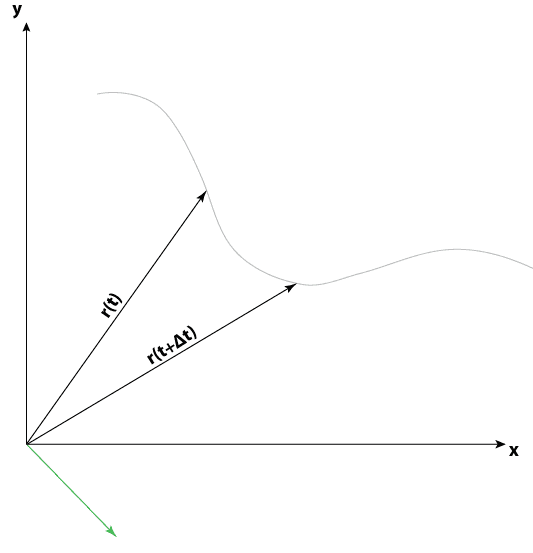
I'm inclined to say the latter, because substraction of two vectors must be a vector in that same vector space. So, in my mind, [tex]\dot{r}(t)[/tex] looks like an ordinary parametric vector-valued function, and not a vector field. Just a function, where all the tails of vectors are at the origin, just like [tex]r(t)[/tex]. If it were a vector field, it would have to use coordinates [tex]x[/tex] and [tex]y[/tex] as a part of its definition, right? You would have to see it clearly from a definition, it has to be [tex]\dot{r}(x,y)[/tex] in order to be a vector field. But it doesn't, so it's not.
So, what am I missing here?
--
Also, this could be an indication of a bigger problem I'm having, namely, an understanding of a substraction of vectors. You see, when I think of a vector space in [tex]R^{3}[/tex], I see this
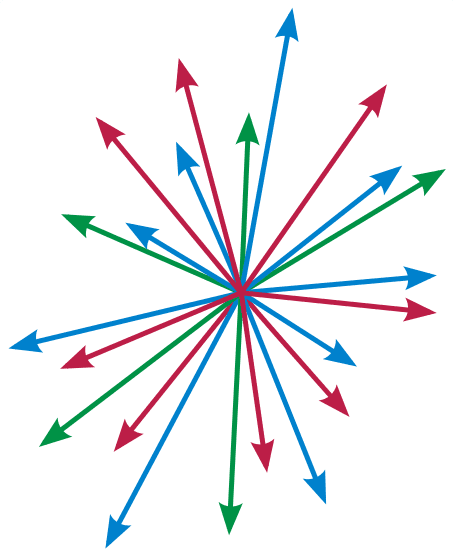
So, a substraction of two vectors is
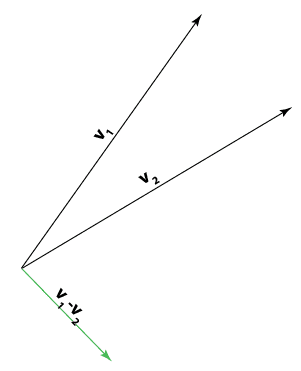
but one of the most common pictures of substraction is
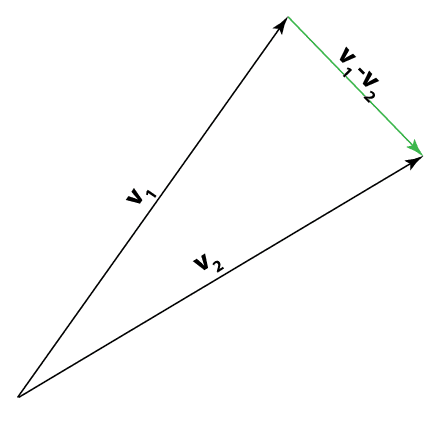
I'm having problems with this picture, and it's the most normal thing we use in engineering or physics all the time. What exactly is this [tex]v_{1}-v_{2}[/tex] in the second picture?
It clearly doesn't belong to the vector space where [tex]v_{1}[/tex] and [tex]v_{2}[/tex] belong, otherwise its tail would be at the same starting point. It looks like it's detached from all the other vectors, like it's an element of a new vector space, whose starting point is a tip of a vector [tex]v_{1}[/tex]. How do you explain this mathematically?
I hope I made at least a little sense, and thanks in forward for all the help I can get.
I thought about putting this topic in physics subforum, but I think it's overall more fitting here.
So, I'm having problems understanding some basic stuff, and I'm kinda embarassed. I'm an engineer and I'm trying to sort things I already know but on a more rigorous mathematic foundation, and then I get confused from time to time, such as now.
Anyway, let's say we have a parametric vector-valued function [tex]r(t)=(x(t),y(t))[/tex]
Nothing too fancy, just your everyday normal trajectory. Now, if we define a derivative of this function as
[tex]\dot{r}(t)=\frac{dr(t)}{dt}=(\dot{x}(t),\dot{y}(t))[/tex]
it is said that this represents the velocity of a function in all the points of the curvature [tex]r(t)[/tex].
Therefore, it must be a vector field, by its nature. And now that I think about it, I can't seem to understand this. For something to be a vector field, it must have an input vector and an output vector. For me, [tex]\dot{r}(t)[/tex] is just another parametric vector-valued function, with a scalar as an input, that's all I see.
Moreover, let's recall the definition of a derivative
[tex]\dot{r}(t)=\frac{dr(t)}{dt}=lim_{\Delta t \rightarrow 0} \frac{r(t + \Delta t) - r(t)}{\Delta t}[/tex]
But what exactly is [tex]{r(t + \Delta t) - r(t)[/tex]? Is it this?
or this?
I'm inclined to say the latter, because substraction of two vectors must be a vector in that same vector space. So, in my mind, [tex]\dot{r}(t)[/tex] looks like an ordinary parametric vector-valued function, and not a vector field. Just a function, where all the tails of vectors are at the origin, just like [tex]r(t)[/tex]. If it were a vector field, it would have to use coordinates [tex]x[/tex] and [tex]y[/tex] as a part of its definition, right? You would have to see it clearly from a definition, it has to be [tex]\dot{r}(x,y)[/tex] in order to be a vector field. But it doesn't, so it's not.
So, what am I missing here?
--
Also, this could be an indication of a bigger problem I'm having, namely, an understanding of a substraction of vectors. You see, when I think of a vector space in [tex]R^{3}[/tex], I see this
So, a substraction of two vectors is
but one of the most common pictures of substraction is
I'm having problems with this picture, and it's the most normal thing we use in engineering or physics all the time. What exactly is this [tex]v_{1}-v_{2}[/tex] in the second picture?
It clearly doesn't belong to the vector space where [tex]v_{1}[/tex] and [tex]v_{2}[/tex] belong, otherwise its tail would be at the same starting point. It looks like it's detached from all the other vectors, like it's an element of a new vector space, whose starting point is a tip of a vector [tex]v_{1}[/tex]. How do you explain this mathematically?
I hope I made at least a little sense, and thanks in forward for all the help I can get.