- #1
AzureSekki
- 10
- 0
Summary:: I'm quite stuck on this problem i don't know what I am going to use formula to solve this one
This is the given I am not sure if this is a resolution problem or it involve parallelogram law
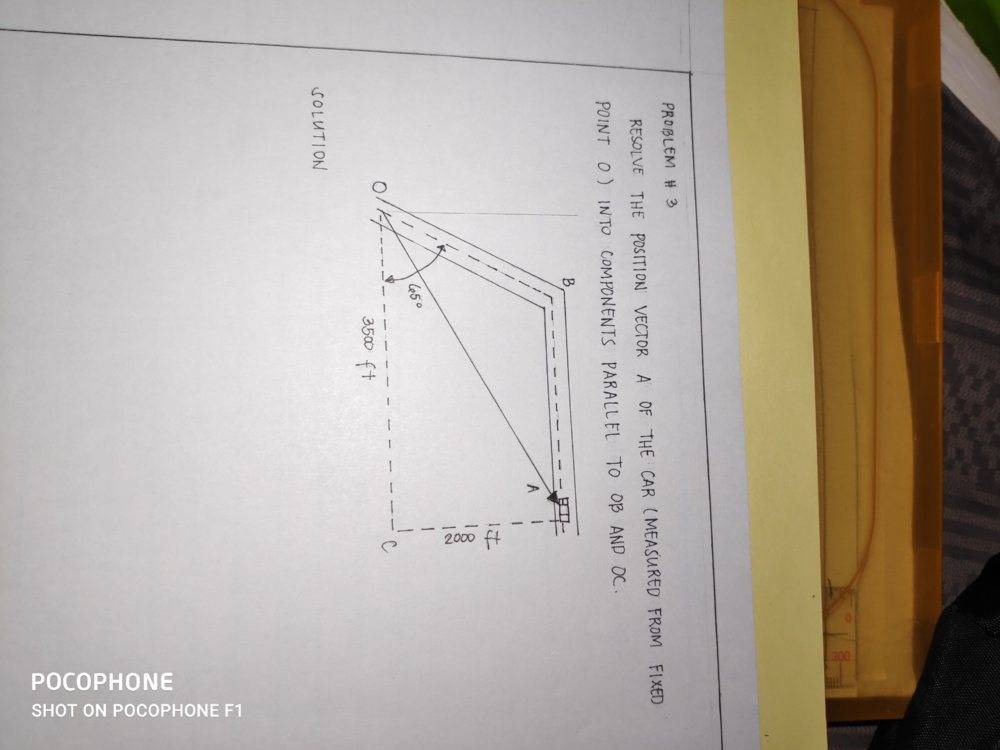

This is the given I am not sure if this is a resolution problem or it involve parallelogram law