sHatDowN
- 52
- 7
- Homework Statement
- Resolve to its component
- Relevant Equations
- vector addition
Determine the amount and type (tensile or compressive) of the spring force so that the resulting force is a vertical force. Also get the resultant force.
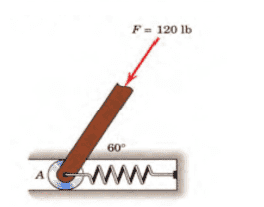
i find 60N (compressive)
and resultant forces is 10800
is that correct?
i find 60N (compressive)
and resultant forces is 10800
is that correct?
