elfmotat
- 260
- 2
Homework Statement
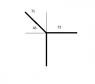
2 weights of 20 N and 10 N are hung from 3 ropes. Find the tension of T1, T2, and T3:

The attempt at a solution
If I designate one of the points as the origin, I get:
T_1sin45+T_2sin0+T_3sin30=30 N
and
T_2cos0+T_3cos30-T_1sin45=0
I'm having trouble finding a third equation... if those two are even right in the first place.
2 weights of 20 N and 10 N are hung from 3 ropes. Find the tension of T1, T2, and T3:
The attempt at a solution
If I designate one of the points as the origin, I get:
T_1sin45+T_2sin0+T_3sin30=30 N
and
T_2cos0+T_3cos30-T_1sin45=0
I'm having trouble finding a third equation... if those two are even right in the first place.