- #1
Stasis
- 3
- 0
Hey all, I've been attempting this all week and can't get my head around what the proper way to calculate the answers for this query is so...
1. Homework Statement
The force shown in the force-time diagram acts on a 3.4 kg object.
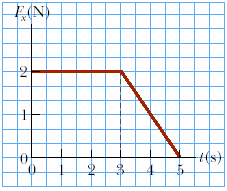
(a) Find the impulse of the force.
(b) Find the final velocity of the mass if it is initially at rest.
(c) Find the final velocity of the mass if it is initially moving along the x-axis with a velocity of -1.8 m/s.
2. Homework Equations
F=ma
Possibly kinematics
Well I got the correct answers already:
A) 8 (area under the line in the graph, (3*2) + (2*2/2)
B) 2.34m/s
C) 0.548
The thing is I accidentally found the answers for this, I decided to start with the acceleration via:
A=F/M
A1=1.764
A2=0.59
On a whim I added these together and submitted (practice server) and it was correct, I repeated this a few times and it was always correct.
For C) I just removed this value from my answer from B)
What is the correct way I should have done this? I can't seem to work out the result any other way :S
Any help is appreciated.
1. Homework Statement
The force shown in the force-time diagram acts on a 3.4 kg object.
(a) Find the impulse of the force.
(b) Find the final velocity of the mass if it is initially at rest.
(c) Find the final velocity of the mass if it is initially moving along the x-axis with a velocity of -1.8 m/s.
2. Homework Equations
F=ma
Possibly kinematics
The Attempt at a Solution
Well I got the correct answers already:
A) 8 (area under the line in the graph, (3*2) + (2*2/2)
B) 2.34m/s
C) 0.548
The thing is I accidentally found the answers for this, I decided to start with the acceleration via:
A=F/M
A1=1.764
A2=0.59
On a whim I added these together and submitted (practice server) and it was correct, I repeated this a few times and it was always correct.
For C) I just removed this value from my answer from B)
What is the correct way I should have done this? I can't seem to work out the result any other way :S
Any help is appreciated.