Velocity of spheres after collision

[Saitama]

Homework Statement

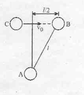
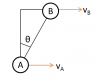
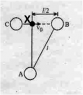
Three spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible inelastic cord of length / and are at rest in the position shown when sphere B is struck directly by sphere C which is moving to the right with a velocity $v_o$. Knowing that the cord is taut when sphere B is struck by sphere C and assuming perfectly elastic impact between B and C, determine the velocity of each sphere immediately after impact.

Homework Equations

The Attempt at a Solution

Let the velocity of A, B and C after collision be $v_A$, $v_B$ and $v_C$ respectively.

Conserving linear momentum,
$mv_0=mv_A+mv_B+mv_C$

As the string is inextensible, the components of velocity of A and B along the string should be equal i.e $v_A\sin\theta=v_B\sin\theta \Rightarrow v_A=v_B$ but this is wrong because as per the answer key the velocities of A and B are different.

 

[consciousness]

Hmm interesting question I think that the problem lies in the directions you have decided for the velocities of A and B. How can the velocity of A have a component perpendicular to the string if the tension can only provide impulse to it? Also for B the tension will give an impulse and the velocity vector won't be parallel to Vo. You have to use vector equations for conservation of linear momentum.

 

[haruspex]

As the string is inextensible, the components of velocity of A and B along the string should be equal

It's a string, not a rod.

 

[Saitama]

Let the velocity of B in horizontal and vertical direction be $v_{Bx}$ and $v_{By}$ and similarly for A, $v_{Ax}$ and $v_{Ay}$

Conserving momentum in the horizontal direction,
$mv_o=mv_{Ax}+mv_{Bx}+mv_C$

Conserving momentum in the vertical direction,
$0=mv_{Ay}+mv_{By} \Rightarrow v_{By}=-v_{Ay}$

I still need more equations to solve the problem. I can only think of conserving energy.
$$\frac{1}{2}mv_o^2=\frac{1}{2}mv_C^2+\frac{1}{2}m(v_{Ax}^2+v_{Ay}^2)+ \frac {1}{2}m(v_{Bx}^2+v_{By}^2)$$
$$\Rightarrow v_o^2=v_C^2+v_{Ax}^2+2v_{Ay}^2+v_{Bx}^2$$

Is it right to assume that C moves only in horizontal direction even after the collision?
As the collision is elastic, $v_o=v_{Bx}-v_{C}$.

Am I doing this right? I still need more equations.

 

[consciousness]

One equation is to equate the velocities along the string. As it is an elastic collision don't use conservation of energy just use coefficient of restitution as energy conservation gives complicated equations and the same result as coefficient of restitution.

EDIT:

And yes C will move in horizontal direction only as no vertical impulse acts on it. We have 5 unknowns and 5 equations but I don't think we will get the answer as conserving energy isn't a "unique equation" and using coefficient of restitution is the same thing.

 

[Saitama]

One equation is to equate the velocities along the string.

I think I cannot do that. Check haruspex's post.

 

[consciousness]

I think I cannot do that. Check haruspex's post.

Well I thought that since the string remains tight after the collision the components along it would be equal. As for how it remains tight I don't have any mathematical reason but I cannot imagine practically how the the string would become loose after the collision.

 

[haruspex]

Well I thought that since the string remains tight after the collision the components along it would be equal. As for how it remains tight I don't have any mathematical reason but I cannot imagine practically how the the string would become loose after the collision.

Ive come around to your view. Initially, at least, it will remain taut. And since it is taut before the collision, you can treat the collision as work conserving.

$v_o=v_{Bx}-v_{C}$

No, that ignores the role of A. Consider KE of whole system.

 

[Saitama]

No, that ignores the role of A. Consider KE of whole system.

Does this mean I can conserve energy in this problem?

And can I equate the components of velocity of A and B along the string?

 

[haruspex]

Does this mean I can conserve energy in this problem?

And can I equate the components of velocity of A and B along the string?

Yes, I think you can justify both of those.

 

[Saitama]

Yes, I think you can justify both of those.

I wrote the equation for conservation of energy in post #4.

(I have assumed that x component of velocity both A and B is in the right direction and y-component in vertically upward direction)
Equating the components of velocity along the string,
$$v_{By}\cos \theta+v_{Bx}\sin \theta=v_{Ax}\sin \theta+v_{Ay}\cos \theta$$
$$(v_{Bx}-v_{Ax})\sin \theta=2v_{Ay}\cos \theta$$

From the figure, $\sin \theta=1/2$ and $\cos \theta=\sqrt{3}/{2}$
$$\Rightarrow v_{Bx}-v_{Ax}=2\sqrt{3}v_{Ay}$$

That's going to be really dirty.

Can you give me a few ideas how should I begin to solve this? I have got enough equations I think but substituting expressions in the energy equation gives so many squared terms.

 

[haruspex]

I have got enough equations I think but substituting expressions in the energy equation gives so many squared terms.

When you substitute in the energy equation, you should find a common factor (a velocity) that cancels out, reducing it to a linear form.

 

[Saitama]

When you substitute in the energy equation, you should find a common factor (a velocity) that cancels out, reducing it to a linear form.

I had $v_o=v_{Ax}+v_{Bx}+v_C \Rightarrow v_C=v_o-(v_{Ax}+v_{Bx})$
Also $v_{Bx}-v_{Ax}/2\sqrt{3}=v_{Ay}$

Substituting them in the energy equation,
$$v_o^2=v_o^2+v_{Ax}^2+v_{Bx}^2-2v_o(v_{Ax}+v_{Bx})+\frac{v_{Bx}^2+v_{Ax}^2-2v_{Ax}v_{Bx}}{6}+v_{Bx}^2$$
$$\Rightarrow 12v_o(v_{Ax}+v_{Bx})=7v_{Ax}^2+19v_{Bx}^2-2v_{Ax}v_{Bx}$$
I don't see how can I simplify that.

 

[ehild]

One equation is still missing: conservation of angular momentum.

ehild

 

[Saitama]

One equation is still missing: conservation of angular momentum.

ehild

About what point should I do this?

About A?

 

[ehild]

I would do it around the point above C, in the horizontal line between A and B. But A is good, too.

 

[Saitama]

I would do it around the point above C, in the horizontal line between A and B.

I am assuming the point X shown in attachment.

About that point,
$$0=\frac{mv_{By}\ell}{2}+\frac{mv_{Ax}\sqrt{3}\ell}{2}$$
$$\Rightarrow v_{By}=-\sqrt{3}v_{Ax}$$

Correct?

 

[ehild]

correct

 

[Saitama]

correct

I further solved it but I am not able to reach the right answer.

I had $v_{Bx}-v_{Ax}x=2\sqrt{3}v_{Ay}$. As $v_{By}=-\sqrt{3}v_{Ax}=-v_{Ay}$

$$v_{Bx}-v_{Ax}=6v_{Ax} \Rightarrow v_{Bx}=7v_{Ax}$$

From the energy equation:
$$12v_o(v_{Ax}+v_{Bx})=7v_{Ax}^2+13v_{Bx}^2-2v_{Ax}v_{Bx}$$
$$\Rightarrow 12v_o(8v_{Ax})=(7+13\times 49-14)v_{Ax}^2$$
$$\Rightarrow v_{Ax}=\frac{16v_o}{105}$$

$$v_A=\sqrt{v_{Ax}^2+v_{Ay}^2}=2v_{Ax}=\frac{32v_o}{105}$$

But this is wrong.

 

[ehild]

You might have an error in the energy equation. Check.

ehild

 

[Saitama]

You might have an error in the energy equation. Check.

ehild

I did find a mistake in the energy equation [strike]but I still do not end up with the right answer[/strike] .

I will make the equations again.
I had $v_C=v_o-(v_{Ax}+v_{Bx})=v_o-8v_{Ax}$
$\Rightarrow v_C^2=v_o^2+64v_{Ax}^2-16v_ov_{Ax}$

From the energy equation,
$$v_o^2=v_C^2+v_{Ax}^2+2v_{Ay}^2+v_{Bx}^2$$
$$\Rightarrow v_o^2=v_o^2+64v_{Ax}^2-16v_ov_{Ax}+v_{Ax}^2+2(\sqrt{3}v_{Ax})^2+49v_{Ax}^2$$

Solving this, I get $v_{Ax}=2v_o/15$ and therefore $v_{A}=2v_{Ax}=4v_o/15$ which is correct as per the answer key.

$$v_C=v_o-8v_{Ax}=v_o-\frac{16}{15}v_o=\frac{-v_o}{15}$$

I have $v_{Bx}=7v_{Ax}=14v_o/15$ and $v_{By}=-\sqrt{3}v_{Ax}=-2\sqrt{3}v_o/15$
Hence,
$$v_B=\sqrt{v_{Bx}^2+v_{By}^2}=\frac{v_o}{15}\sqrt{196+12}=\frac{\sqrt{208}v_o}{15}$$

Thank you ehild and haruspex!

 

[Arnav jamale]

What should I do if collision was head on inelastic

 

[Arnav jamale]

Reply fast

 

[haruspex]

What should I do if collision was inelastic

I assume you mean completely inelastic. What can you think of? What equation would you have instead?

 

[Arnav jamale]

Conservation of linear momentum but we can't conserve kinetic energy

 

[Arnav jamale]

So I just want is it possible to determine velocity of sphere B

 

[haruspex]

Conservation of linear momentum but we can't conserve kinetic energy

Yes, but there is another equation available. If two bodies collide, head-on, completely inelastically, what do you know about their subsequent velocities?

 

[Arnav jamale]

Do you mean one dimension equation which tell us final velocities after collision which also contains coefficient of restitution

 

[Arnav jamale]

But this oblique collision and we don't have coefficient of restitution

 

[haruspex]

But this oblique collision and we don't have coefficient of restitution

The set up in post #1 is not oblique. Maybe your problem is different.
Completely inelastic means the coefficient is zero.

 

[Arnav jamale]

My setup is same but it's not perfectly inelastic it's just head on inelastic

 

[haruspex]

it's just head on inelastic

I do not know what you mean by that. Is it a head on collision or oblique?