Javad
- 35
- 2
- Homework Statement
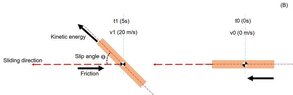
- Two equal metal strips (the same material, the same size and mass, mass for each one is 500 g, and size for each one is 50cm* 5cm) are pushed on a straight rigid surface to reach the same velocity (v1 = 20m/s) at the same time (t1, 5s), then we let them freely continue sliding. Object A slides while the sliding direction is along the longitudinal centerline of the object, object B slides while it rotates about its central-vertical axis to make an angle (ϴ = 45°) between the sliding direction and the longitudinal centerline of the object. Which object will stop sooner (which object will travel a shorter distance (d))?
- Relevant Equations
- F=ma
Kinetic energy = 1/2mv²
Power = Fv
d = vt + 1/2at²
d = 1/2 (v + v˳)t
Fᵪ=F.cosθ