Very hard modelling and problem solving Calculus Question

[LBrenda16]

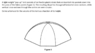
A light-weight "pop-up" tent consists of six flexible plastic struts that are inserted into pockets sewn into the joins of the fabric panels. The resulting shape has hexagonal horizontal cross-sections, while vertical cross-sections through the centre are semi-circular.

Derive a formula for the volume of the tent as a function of its height.

How do i do it? I tried doing a symmetrical trapezium on the graph and revolved it around half way to get the tent look, not a sphere, but the top part (the roof of the tent) was in the shape of a trapezium (shaped like a diamond? like there's edges), not half a sphere like it should be, and the base being a hexagon. If you can imagine it? Anyways, need help!

Attached is the question and the picture of the tent.

 

[mfb]

Can you use a volume integral?

It is sufficient to consider 1/6 or 1/12 of the tent, of course.

The result looks very nice.

 

[henpen]

You can avoid explicit volume integration if you're clever (and get it right, which perhaps I haven't):

Note that the base of a 1/6 of the tent is an equilateral triangle, sides of length $l$ (which is h at its maximum), and area$\frac{\sqrt{3}}{4}l$. http://gyazo.com/6ce4bd547e7a5a47fc89a45ad586f79b Note that
$$l^2+x^2=h^2$$
$$l=\sqrt{h^2-x^2}$$

$$\int_{x=0}^{x=h}\frac{\sqrt{3}}{4}ldx=\frac{\sqrt{3}}{4}\int_{x=0}^{x=h}\sqrt{h^2-x^2}dx$$
Integrate:
$$x=h \cos(u)$$
$$dx=-h \sin(u)du$$
$$\frac{\sqrt{3}}{4}\int_{x=0}^{x=h}\sqrt{h^2-h^2 \cos^2(u)}(-h \sin(u))du=\frac{-h^2 \sqrt{3}}{4}\int_{x=0}^{x=h}(\sin^2(u) )du$$
$$x=h, u=0$$
$$x=0, u=\frac{\pi}{2}$$
$$\frac{h^2 \sqrt{3}}{4}\int_{0}^{\frac{\pi}{2}}(\sin^2(u) )du=\frac{h^2 \sqrt{3}}{4}\frac{\pi}{4}$$

Multiply by 6 for the whole thing.

 

[mfb]

Well, two parts of the volume integral are trivial, so you just have to calculate an easy 1-dimensional integral there as well.

I think there is an $l$ missing in your formula of the triangle area.
I used a different coordinate for the non-trivial integral.

 

[henpen]

Well, two parts of the volume integral are trivial, so you just have to calculate an easy 1-dimensional integral there as well.

I think there is an $l$ missing in your formula of the triangle area.
I used a different coordinate for the non-trivial integral.

You're right- the integral is much simpler, just a polynomial.