Video on imaginary numbers and some queries

[PainterGuy]

Hi,

I was watching the following video. I found some points confusing. Could you please help me to understand the gaps? Thanks, in advance!


Question 1:

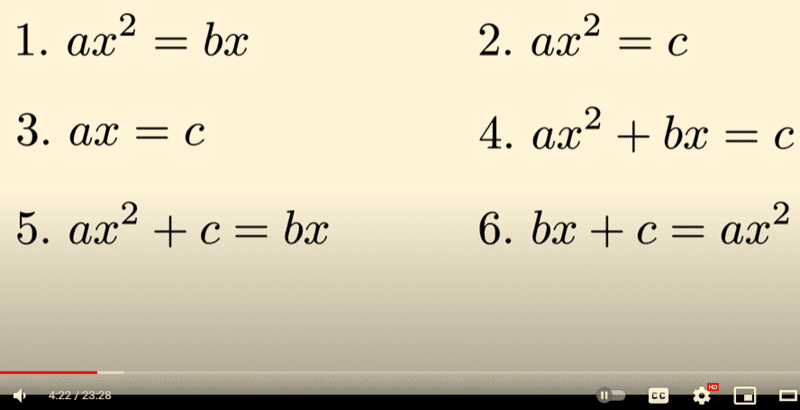
Around 4:22, the video says the following.
So for those mathematicians, negative numbers didn't exist. You could subtract, that is find the difference between two positive quantities, but you couldn't have a negative answer or negative coefficients. Mathematicians were so averse to negative numbers that there was no single quadratic equation. Instead, there were six different versions arranged so that the coefficients were always positive.

I don't understand why having all the coefficients positive was so important. For example, the equation shown below has one negative coefficient and has one solution positive and one negative. Okay, you can throw out the negative solution but you're still left with one 'good' solution.

13x²-7x=7

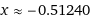
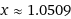
Source: https://www.wolframalpha.com/input/?i=solve+13x^2-7x-7=0,xQuestion 2:

Around 6.08 the video says the following.
For nearly two decades, del Ferro keeps his secret. Only on his deathbed in 1526 does he let it slip to his student Antonio Fior. Fior is not as talented a mathematician as his mentor, but he is young and ambitious. And after del Ferro's death, he boasts about his own mathematical prowess and specifically, his ability to solve the depressed cubic. On February 12, 1535, Fior challenges mathematician Niccolo Fontana Tartaglia
who has recently moved to Fior's hometown of Venice.
...
As is the custom, in the challenge Tartaglia gives a very discernment of 30 problems to Fior. Fior gives 30 problems to Tartaglia, all of which are depressed cubics. Each mathematician has 40 days to solve the 30 problems they've been given. Fior can't solve a single problem. Tartaglia solves all 30 of Fior's depressed cubics in just two hours.Even if Fior was not a good mathematician, it's still surprising that he wasn't able to solve a single problem in spite of knowing an algorithm to solve depressed cubic. Why was it so?Question 3:

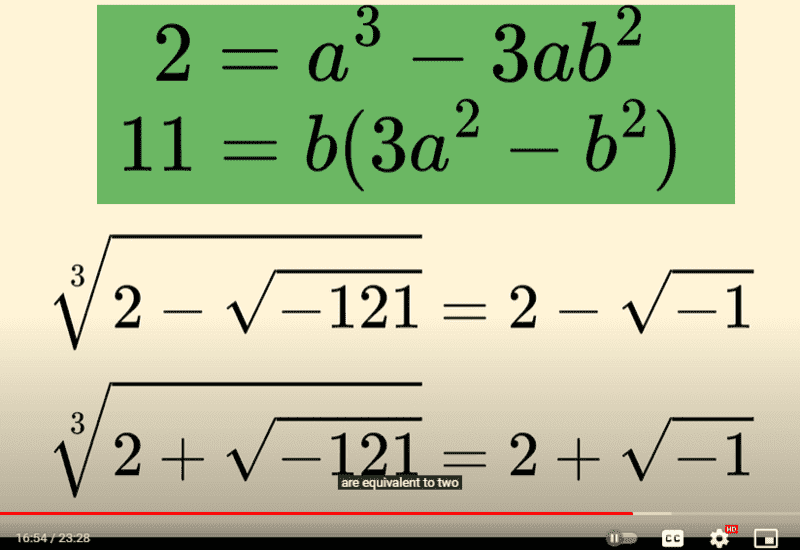
Where are those equations in green coming from? Could you please help me?

 

[PeroK]

1) I'm sure you can read about it and find out. It depresses me to see these centuries of stumbling in the dark, blind to the power of mathematics. If they could just have opened their minds...

2) No idea.

3) I assume those are the equations for $a, b$ that come from the cubic formula for the roots. You'll need to work through the problem yourself.

 

[FactChecker]

1) They didn't even believe in negative numbers, only positive numbers. It's not just the negative solution that was a problem for them, they didn't believe in negative numbers in the problem statement. The number 0 was not even discovered until around 650 A.D.
2) You are over-estimating their capability back then. Equations as we know it did not exist. They only had verbal statements of the process to solve a problem. Any process had to use only real, observable, objects. So if the process used imaginary things, it was not conceived.
3) It looks like the equations came from the 2 and the $\sqrt {-121} = \sqrt {-(11^2)}$ in the video. Those people were very clever and worked very hard to solve these problems. I will not even try to reinvent their methods.

 

[Astronuc]

I encountered the video in the OP this morning. I remember learning some of the history more than 50 years ago, but didn't know of the rivalries.

As is the custom, in the challenge Tartaglia gives a very discernment of 30 problems to Fior. Fior gives 30 problems to Tartaglia, all of which are depressed cubics. Each mathematician has 40 days to solve the 30 problems they've been given. Fior can't solve a single problem. Tartaglia solves all 30 of Fior's depressed cubics in just two hours.Even if Fior was not a good mathematician, it's still surprising that he wasn't able to solve a single problem in spite of knowing an algorithm to solve depressed cubic. Why was it so?

I am intrigued by this matter, but it appears that Tartaglia could 'see' the problem. Starting at 8:00 in the video, the narrator walks through the problem x³ + 9x = 26, an example of a depressed cubic. The volume of a cube is x³, then one extends the sides by length y, to obtain a volume (x+y)³ = z³, which one sees at 8:32 in the video. The extended cube has 8 shapes: the original cube x³, two sets of three right prisms of equal shape (x²y and xy²), and new cube of y³. The two sets of three right prisms for another right prism of height x, length z = (x+y) and width 3y, (9:06 in the video). The volume of that shape is 3xzy, or 3x(x+y)y.

Some folks can see patterns in numbers, equations, data, information.

Clearly a minority of the population is adept at mathematics and/or physics, but most are not. The why is an interesting question that I have pondered for more than 60 years after observing so many fellow students struggle with STEM over the years.

https://en.wikipedia.org/wiki/Scipione_del_Ferro
https://en.wikipedia.org/wiki/Nicolo_Tartaglia
https://en.wikipedia.org/wiki/Gerolamo_Cardano

https://en.wikipedia.org/wiki/Ars_Magna_(Cardano_book), 1545

https://en.wikipedia.org/wiki/Cubic_equation

https://community.wolfram.com/groups/-/m/t/3036063


https://www.quantamagazine.org/the-scandalous-history-of-the-cubic-formula-20220630/


Imagine that!
https://en.wikipedia.org/wiki/Rafael_Bombelli