Virial Theorem for an expanding globular cluster

[Barbequeman]

Homework Statement

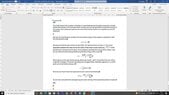
You may make the assumption that the gas and stars are distributed as sphere of constant density and some finite radius rc. The total mass of the stars and of gas is different: assume that the total mass of the gas, Mg, is given by Mg = f M*, where M* is the total mass of the stars.

Start by assuming that the system overall is unrotating and in equilibrium. Calculate the kinetic energy of the stars in terms of rc, f, and M*. Therefore also calculate the total energy of the system.

Relevant Equations

2K+U=0 the basic equation for the virial theorem in a system which is unrotating and in equilibrium

I attached a file which shows my attempt to resolve this problem with the possible two pair interaction which gives us the kinetic energy of the cluster in an expanding system, at least I think so. But to be honest I´m more or less completely stuck with this question and I would be glad if somebody could explain me how to use the virial theorem in this special case.

 

[ergospherical]

The overall reasoning looks good but I'm unsure how the question is supposed to be interpreted. The total (gas + star) mass is $(1+f)M^*$ and it looks as if they'd like us to distribute that uniformly over a sphere of radius $r_c$. That would have a gravitational potential energy of\begin{align*}
\Omega = \dfrac{-3G(1+f)^2 {M^*}^2}{5r_c}
\end{align*}Then, assuming the gas to have negligible kinetic energy would imply that the mean square speed $\langle v^2 \rangle$ of the stars is\begin{align*}
\langle v^2 \rangle = \dfrac{2T}{M^*} = \dfrac{-\Omega}{M^*} = \dfrac{3G(1+f)^2 M^*}{5r_c}
\end{align*}I don't know which way is right...

 

[Barbequeman]

I think I resolved it with the help of my friend from the university to crack the kinetic energy question which is the

 

[Barbequeman]

The next question would be how to resolve towards f, at what gas fraction f the cluster is disrupted

The question in according to our Book is
Now suppose that winds from young stars and supernovae explosions very rapidly (you can assume instantaneously) expel the gas from the system. At what gas fraction f is the cluster disrupted?

With best wishes and thank you for your help