Visualization of Integration by Parts

[Lancelot1]

Hello all,

I am trying to understand the rational behind the visualization of integration by parts, however I struggle with it a wee bit.

I was trying to read about it in Wiki, this is what I found:

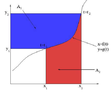
View attachment 7307View attachment 7308

-----------------------------------------------------------------------------------------------------------------------------------------
In general I don't understand why this visualization was chosen, but to be more specific on the details, I don't understand why

\[x_{2}y_{2}-x_{1}y_{1}=xy\]

I also don't understand how can one claim an integral to be the area on the left and not under the curve.

I would appreciate it if you guys could explain this to me. I understand how to use integration by parts, I also understand the proof (although wasn't sure: can you always say that an integral of derivative of some function is the function?). I mainly don't get the visualization, and really want to.

Thank you in advance !

 

[I like Serena]

In general I don't understand why this visualization was chosen, but to be more specific on the details, I don't understand why

\[x_{2}y_{2}-x_{1}y_{1}=xy\]

Hey Lancelot! (Wave)

It's really a shorthand for:
\[ x\cdot y(x)\Big|_{x_1}^{x_2} = x_{2}y_{2}-x_{1}y_{1} \]
or alternatively
\[ x(y)\cdot y\Big|_{y_1}^{y_2} = x_{2}y_{2}-x_{1}y_{1} \]
dependending on whether we see y as a function of x, or x as a function of y.

I also don't understand how can one claim an integral to be the area on the left and not under the curve.

I would appreciate it if you guys could explain this to me. I understand how to use integration by parts, I also understand the proof (although wasn't sure: can you always say that an integral of derivative of some function is the function?). I mainly don't get the visualization, and really want to.

Remember that it's a visualization.
It means that we can play around a bit with where we put an area, rotating it, or reflecting it, as we see fit.
The blue area does respond to the integral 'under' the graph - just with respect to the y-axis.
Note that the integral is with respect to y instead of with respect to x.
So we must consider the y-axis to be horizontal (consider the reflection in the line y=x that will make it so).
After that the area is indeed under the graph.

 

[Lancelot1]

Thank you.

This is difficult. How come you can just change xy(x) to xy ? Just like that ?

I see your point, it makes sense, I just struggle to understand when can I use shortcuts like this.

 

[Joppy]

Thank you.

This is difficult. How come you can just change xy(x) to xy ? Just like that ?

I see your point, it makes sense, I just struggle to understand when can I use shortcuts like this.

It might be helpful to draw up a graph on paper, look at the area under the curve on the x-axis, and then (physically) rotate your paper and try do the same thing for the y-axis.

 

[I like Serena]

Thank you.

This is difficult. How come you can just change xy(x) to xy ? Just like that ?

I see your point, it makes sense, I just struggle to understand when can I use shortcuts like this.

It's not really a shortcut -- it's a shorthand.

What makes it a bit confusing is that x and y both have 2 different meanings that are used interchangeably.
x is sometimes a function of y, and sometimes a free variable.
In math we'd normally make a distinction somehow, for instance by writing $\tilde x$ when we mean the function, and just $x$ for the free variable. Still, we can see and deduce the meaning from how the symbols are used.

When can we use shorthands like these?
Whenever we want to - just remember they are shorthands, and remember what they stand for.
In particular the partial integration theorem is a bit shorter, more readible, and more memorable if we write it like $\int udv=uv - \int vdu$.