arhzz
- 283
- 57
- Homework Statement
- Multiple parts
- Relevant Equations
- Capacitor
Hello!
Consider this circuit;
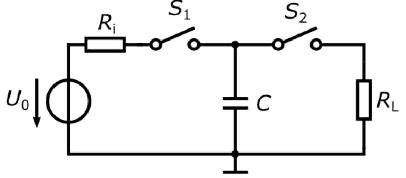
Now this is what happens with the circuit;
i)At time t0, switch S1 is closed and the capacitor has its maximum capacity at this time C = Cmax
ii)At time t1 the switch is opened
iii)Due to the mechanical vibration, the electrodes are drained from the capacitor at time t2, so the capacity is minimal at time t3. Assume that the capacitance changes linearly
iv)At time t4, switch S2 is closed
v)Thereafter, the capacitor electrodes are pushed together again with the switch open and the cycle begins again
a)For each of the states, state the voltage on the capacitor at the end of the respective process. You may assume that the stationary state is reached at each step. Cmax = 2 Cmin
b) Give a diagram of the Voltage
c) How big is the generated electrical energy? Cmin = 200pF U = 10V (the points in time t2 and t3 are decisive for this sub-item)
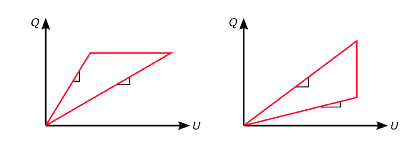
d)The figures below show two possible cycle processes in a Q-U diagram. Select a cyclic process and enter the points in time t1-t5,and write out the gradients;
Okay so a) is already giving me trouble; What is particularly bothering me is the fact that we have to assume that at the end of each step (so t1 t2 t3..etc) the stationary state has been reached (so either the capacitor is fully charges or discharged).
i) Uc = Uo --> My thought process is that since the current is going directly into the capacitor and if we assume that at the end of t1 stationary state has been reached than it should be that it is fully loaded,meaning the supply voltage Uo
ii) Uc = Uo --> Since S2 is still not closed the capacitor cannot discharge over teh RL on the right,so the voltage should stay the same
iii) Here I am having problems,I think that the voltage is shrinking,the capacitor is discharging,but since we are interested in the stationary state what will that voltage be? I'd say its 0,but can we have Cmin when the voltage across the capacitor is 0?
iv) Uc = 0 --> since S2 is closed the capacitor should discharge over the RL
v) Here I really don't have an idea.
b) Dont think I can do it without a)
c) I tried it like this. I first calculated what the Energy is at t2. C = Cmax at that point so ( we are also given a tiny graph and that makes it pretty clear) so Cmax = 400pF. Use this formula
$$ W_1 = \frac{C_{max} U^2}{2} $$ that gives me W1 = 20 nJ
Now we can calculate the charge; $$ Q = C*U $$ C = 4 nC
Now the charge remains the same but the voltage changes as well does the capacity; I calculated the new voltage like this;
$$U_n = \frac{Q}{C_{min}} $$ I get 20V
Now plug this into W2 (and the new C which is Cmin) I get W2 = 40 nJ
so ## \delta W = 20 nJ ##
and for d) I think it is the picture on the left,although I am not certain ( hard to figure out without part a)
Any advice for part a) ? Also what do you think about the way I tackled c) ?
Thanks for the help and excuse the long post.
Consider this circuit;
Now this is what happens with the circuit;
i)At time t0, switch S1 is closed and the capacitor has its maximum capacity at this time C = Cmax
ii)At time t1 the switch is opened
iii)Due to the mechanical vibration, the electrodes are drained from the capacitor at time t2, so the capacity is minimal at time t3. Assume that the capacitance changes linearly
iv)At time t4, switch S2 is closed
v)Thereafter, the capacitor electrodes are pushed together again with the switch open and the cycle begins again
a)For each of the states, state the voltage on the capacitor at the end of the respective process. You may assume that the stationary state is reached at each step. Cmax = 2 Cmin
b) Give a diagram of the Voltage
c) How big is the generated electrical energy? Cmin = 200pF U = 10V (the points in time t2 and t3 are decisive for this sub-item)
d)The figures below show two possible cycle processes in a Q-U diagram. Select a cyclic process and enter the points in time t1-t5,and write out the gradients;
Okay so a) is already giving me trouble; What is particularly bothering me is the fact that we have to assume that at the end of each step (so t1 t2 t3..etc) the stationary state has been reached (so either the capacitor is fully charges or discharged).
i) Uc = Uo --> My thought process is that since the current is going directly into the capacitor and if we assume that at the end of t1 stationary state has been reached than it should be that it is fully loaded,meaning the supply voltage Uo
ii) Uc = Uo --> Since S2 is still not closed the capacitor cannot discharge over teh RL on the right,so the voltage should stay the same
iii) Here I am having problems,I think that the voltage is shrinking,the capacitor is discharging,but since we are interested in the stationary state what will that voltage be? I'd say its 0,but can we have Cmin when the voltage across the capacitor is 0?
iv) Uc = 0 --> since S2 is closed the capacitor should discharge over the RL
v) Here I really don't have an idea.
b) Dont think I can do it without a)
c) I tried it like this. I first calculated what the Energy is at t2. C = Cmax at that point so ( we are also given a tiny graph and that makes it pretty clear) so Cmax = 400pF. Use this formula
$$ W_1 = \frac{C_{max} U^2}{2} $$ that gives me W1 = 20 nJ
Now we can calculate the charge; $$ Q = C*U $$ C = 4 nC
Now the charge remains the same but the voltage changes as well does the capacity; I calculated the new voltage like this;
$$U_n = \frac{Q}{C_{min}} $$ I get 20V
Now plug this into W2 (and the new C which is Cmin) I get W2 = 40 nJ
so ## \delta W = 20 nJ ##
and for d) I think it is the picture on the left,although I am not certain ( hard to figure out without part a)
Any advice for part a) ? Also what do you think about the way I tackled c) ?
Thanks for the help and excuse the long post.