What is the closed volume integral symbol in Microsoft Word?

[STEMucator]

Hi everyone.

I've been curious about a particular symbol, but I've never seen it used or mentioned in any context. I don't really have much information about its usage, so I thought I would ask around and see if anyone knew about its application.

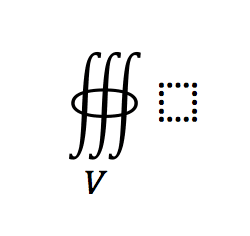
I saw this symbol in Microsoft word.

How do we interpret it, and how do we use it?

I'm familiar with closed surface integrals with differential elements $d \vec S$. We use those when we want to calculate the flux of a field $\vec F$. I'm also familiar with closed surface integrals with differential elements $dS$. We use those when we want to calculate surface area.

What about the closed volume integral above though?

I know we should probably use a differential element $dV$ for a closed volume, and the answer would represent the volume of the object. Is there such thing as a differential volume element $d \vec V$ such that we can extend theorems to the fourth dimension (theorem's like Stoke's theorem and the Divergence theorem)?

Thank you in advance.

 

[jedishrfu]

I think the dash box is simply for inserting your integrand.

Its up to you to remember the dV part.

There is a seldom used math symbol called the delambertian that's used in relativity that is the 4D version of the del operator but this isn't it.

 

[Mark44]

Zondrina, I think you're asking about the integration symbol, not the box to the right. According to this page, https://en.wikipedia.org/wiki/Integral_symbol, that's a closed volume integral. I don't know much more about it, and a quick web search didn't turn up much.

 

[STEMucator]

So the only reason the loop is around the triple integral is to signify the volume is closed.

Does that mean something like the divergence theorem can be written like so:

For a closed volume $V$ such as $x^2 + y^2 + z^2 \leq 1$.

For a volume $V$ that isn't closed such as $x^2 + y^2 + z^2 < 1$, would the theorem would take the form:

Otherwise I don't see any reason to ever have to use the symbol mentioned in the OP.

 

[leright]

I don't know what is meant by "closed volume". What is the difference between a closed volume and an open volume?

 

[HallsofIvy]

In three dimensions there is no such thing as a "closed volume". There can be in higher dimensions, of course.