Volume of a Spherical Pool with Varying Depth

[bmanmcfly]

[SOLVED]A couple of sphere problems

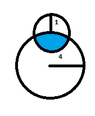
Hi again, I've been studying for my midterms, and in the review exercises I came across a couple questions that have me stumped... How would you guys approach these problems.Ex1: The larger sphere is radius of 4, with the middle point of a second sphere on the skin and to calculate the volume of the larger sphere that would be missing.
View attachment 743
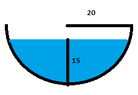
I just wasn't sure where to start on a problem like this, so some pointers on how to approach this would be appreciated...Next, a spherical pool with a radius of 20 meters was filled to where the deepest point was 15 meters deep calculate the volume...

View attachment 744

This one I had a better idea, but wasn't quite sure... I used some trig to start figuring out the volume of the empty space, and then took half the volume of the sphere and took the difference... except I think the intention was to use the volume equation with integration... so, I was just curious how I would figure out an integral to make this calculation??

Once again these are problems that I feel like I should have a handle on, but these got me stumped, just that since there's been multiple similar questions in the review for the midterm suggests that I should be prepared for a similar problem.

Thanks in advance for any help.

 

[MarkFL]

While there are more sophisticated approaches, I would approach both as a solid of revolution problem or volumes by slicing.

Looking at the first problem, can you set up a correct integral representing the volume?

 

[bmanmcfly]

While there are more sophisticated approaches, I would approach both as a solid of revolution problem or volumes by slicing.

Looking at the first problem, can you set up a correct integral representing the volume?

Hi MarkFL, you've been a great help for me since I signed up here... I'm curious what is your field of work? I'm just curious, since you seem to demonstrate a great passion for math to come here and help out dummies like me that are struggling to keep up...

anyway, I misread the first problem...

It was actually a cylinder drilled through the middle of the sphere... and not a sphere from a sphere. Makes the problem a little easier.

To be easier I would orient the cylinder to keep it as a dx.

The solid of revolution method seems to be the intended approach... so, I remember the equation for the circle is the \(\displaystyle y^2+x^2=r^2\) (In this example that would be 16). Since the cylinder is a radius of 1, I'll put the line at y=1.

Now, we find the volume of the cylinder itself + the volume of the spherical cap.

Or, \(\displaystyle dV = \pi y^2 dx + \pi y^2 dx\) one integral for the cylinder, and then from the end where the edge of the sphere is at y=1. the second from that point to the radius, 4.

Should I use the trig to determine the point where the sphere crosses the radius of the cylinder? Part 2 -

So, again with the sphere, this time I got to use dy. The range of y values goes from -15 to -5. So, we turn the x = sqrt( 20^2-y^2 ) Then running the integral...

I seem to have had a simpler time figuring this one out once i had determined a method of attack.

It really does remind me of the joke for engineering students where
In class : 2+2 = 4
The test: y = 2x+5
The exam: Using what you've learned calculate the density of the sun.

Thanks alot, eh.

 

[MarkFL]

I am a retired computer programmer that just enjoys being involved with online math help. This site has attracted the majority of my attention because of the active admins and the feel of community effort.

This is how I would approach the first problem:

I am assuming you are to find the volume of the sphere that is left after drilling the hole through it to make a bead.

Let the radius of the sphere be $r_2$ and the radius of the hole drilled through its center be $r_1$ where $0\le r_1\le r_2$. Let the sphere be centered at the origin. So, we want to revolve the area bounded by:

\(\displaystyle y=r_1\)

\(\displaystyle y=\sqrt{r_2^2-x^2}\)

about the $x$-axis. I would use the washer method. What is the volume of an arbitrary washer? What are the limits of integration? Is there any symmetry we may employ to simplify?

Here is a sketch of the region to be revolved:

 

[bmanmcfly]

I am a retired computer programmer that just enjoys being involved with online math help. This site has attracted the majority of my attention because of the active admins and the feel of community effort.

This is how I would approach the first problem:

I am assuming you are to find the volume of the sphere that is left after drilling the hole through it to make a bead.

Let the radius of the sphere be $r_2$ and the radius of the hole drilled through its center be $r_1$ where $0\le r_1\le r_2$. Let the sphere be centered at the origin. So, we want to revolve the area bounded by:

\(\displaystyle y=r_1\)

\(\displaystyle y=\sqrt{r_2^2-x^2}\)

about the $x$-axis. I would use the washer method. What is the volume of an arbitrary washer? What are the limits of integration? Is there any symmetry we may employ to simplify?

Here is a sketch of the region to be revolved:

OOOOOHHHH! LMAO, another example of how dumb I am... I was trying to use the wrong axis for how I had things orientated, then I remembered if you make y1=y2 then you get the intersection, and everything else fell into place.

So, the way that I would handle like my first post here, the misunderstood example, I guess I would graph it out in such a way that it would be finding the intersections of the the two circles and using the volume of revolution for the two graphs.

I got two days more to review for this midterm, so I may come back with a few more
clarifications on issues...

Like, I understand the rules of derivatives of Log and Ln and e, but I don't really seem to get how they are all connected, and what the significance of these functions workings. If you could point me to something, or I'll come back with a better question.

Until then, thanks a lot for your help, and I truly appreciate your methods of showing the path to the solution.

 

[MarkFL]

...
So, the way that I would handle like my first post here, the misunderstood example, I guess I would graph it out in such a way that it would be finding the intersections of the the two circles and using the volume of revolution for the two graphs...

If I were going to work the first problem as originally stated, I would let my axis of integration, the $x$-axis coincide with the line passing through the centers of the two spheres, and place the origin at the center of the smaller sphere.

The equation for the edge of the cross-section of the smaller sphere is:

\(\displaystyle x^2+y^2=1^2\)

And the equation for the cross-section of the larger sphere is:

\(\displaystyle (x-4)^2+y^2=4^2\)

Subtracting the former from the latter, we find:

\(\displaystyle (x-4)^2-x^2=4^2-1\)

\(\displaystyle x^2-8x+16-x^2=15\)

\(\displaystyle x=\frac{1}{8}\)

And so the volume we seek is given by:

\(\displaystyle V=\pi\left(\int_0^{\frac{1}{8}}8x-x^2\,dx+\int_{\frac{1}{8}}^1 1-x^2\,dx \right)\)

Can you set up the second problem with the correct integral?